Найдем границы интервала устойчивости второго ресурса

Заметим, что при уменьшении времени работы оборудования на 10часов ( Δ b 1= -10) выпуск второй продукции становится отрицательным

x 2 = 50 + 10 Δ b 2 = -50.

Это означает, что такое изменение выводит запас ресурса за интервал устойчивости.

Изменение второго ресурса на величину Δ b 2 будет допустимым, если вызванное им оптимальная программа выпуска будет неотрицательна, т.е. выполняются неравенства: x 1=100 - 20Δ b 2 ≥ 0, x 2=50 + 10Δ b 2 ≥ 0.

Исходя из этих неравенств, найдем максимальное уменьшение и максимальное увеличение второго ресурса.

Найдем максимальное уменьшение второго ресурса 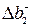. Если запас второго ресурса уменьшается на величину Δ b 2 (Δ b 2 < 0), то выпуск первого продукта увеличивается на 20Δ b 2, а выпуск второго продукта уменьшается на 10 Δ b 2. Отсюда следует, что максимальное уменьшение определяется значением Δ b 2, при котором план второго продукта будет равен 0:

x 2=50 + 10Δ b 2 = 0, Δ b 2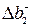=-5, =5.

Найдем максимальное увеличение второго ресурса 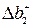. Если запас второго ресурса Δ b 2 увеличивается (Δ b 2 > 0), то выпуск первого продукта уменьшается на 20 Δ b 2, а выпуск второго продукта увеличивается на 10 Δ b 2. Отсюда следует, что максимальное увеличение определяется значением Δ b 2, при котором план первого продукта будет равен 0: x 1=100 - 20Δ b 2 = 0. 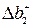=5.

Следовательно, нижняя граница интервала устойчивости

,

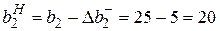верхняя граница интервала устойчивости

.

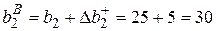Интервал устойчивости будет равен .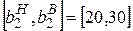

Пример 2.2.2

Пусть запас сырья уменьшается на 100 кг, т.е. Δ b 1 = -100. Новый запас сырья 1000 – 100 = 900 кг. входит в интервал устойчивости [ , 1250]. Тогда новый оптимальный план:

X = { x 1= 100 + 0,6·(-100) = 40, x 2= 50-0,2·(-100)=70, s 1=0, s 2 = 0}.

Выручка на этом плане составит: Z = 9000+4·(-100)=8600.

Пример 2.2.3

Пусть время работы оборудования увеличивается на 10 часов, т.е. D b 2 = 10 и новое время b 2 = 25 + 10 = 35 часов не входит в интервал устойчивости [0,30].

Вопросы для самопроверки

1. Каким свойствам удовлетворяет интервал устойчивости?

2. Дать определение максимального допустимого уменьшения и максимального допустимого увеличения ресурса.

3. Сформулировать теорему об оценке.

4. Чему равна ценность недефицитного ресурса?

Поиск по сайту: