 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение и примеры кривых безразличия
Отношение безразличия ≈ разбивает пространство товаров на классы безразличия: каждый класс безразличия состоит из наборов товаров одинаково привлекательных для потребителя. При этом каждый набор товаров попадает только в один класс безразличия.
Из определения функции полезности следует, что наборы товаров из одного класса безразличия имеют одинаковую полезность:
u(X) = u(Y) = С = const, тогда и только тогда, когда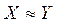 
. (6.2.1)
Для наборов из двух товаров кривая безразличия определяется уравнением
u (x 1, x 2) = C, (6.2.2)
где C – любое число. Множество всех кривых безразличия образуют карту безразличия.
Пример 6. 2.1
Рассмотрим линейную функцию полезности
.
Кривая безразличия определяется уравнением
или 
.
Из этого уравнения следует, что при изменении величины C множество кривых безразличия образуют на плоскости семейство параллельных прямых с углом наклона 
.
Пример 6. 2.2
Пусть функция полезности двух товаров задается равенством
.
Кривая безразличия определяется уравнением 
.
Из этого уравнения следует
,
т.е. множество кривых безразличия образуют на плоскости семейство гипербол (рис. 6.2.1).
Поиск по сайту: