 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ВВЕДЕНИЕ. В настоящем разделе математики рассматриваются математические методы оптимизации при принятии управленческих решений
В настоящем разделе математики рассматриваются математические методы оптимизации при принятии управленческих решений. Для применения этих методов необходимо построить математическую модель некоторой экономической или иной задачи. При этом нужно описать:
1) множество всех альтернатив принятия решений;
2) ограничений, которым должно удовлетворять альтернативные решения;
3) критерий отбора альтернатив (целевая функция).
Наиболее эффективными методами являются методы линейного программирования, в которых целевая функция и все ограничения предполагаются линейными функциями. Для решения некоторых задач применяются методы целочисленного программирования, в которых все или часть переменных должны принимать только целые значения. Наиболее сложными являются модели, в которых целевая функция и ограничения являются нелинейными функциями. Все методы основаны на последовательном (итеративном) поиске оптимального решения.
Раздел 1. Линейное программирование. Основные понятия
| При изучении данного раздела Вам предстоит: 1) Изучить три темы: a. Стандартная и каноническая форма задачи линейного программирования; b. Двойственная задача c. Базисные решения. 2) Ответить на вопросы рубежного теста к разделу 1. При затруднениях с ответом обратитесь к Учебному пособию (Глава 1) или к Глоссарию. |
1.1. Стандартная и каноническая формы задачи линейного программирования
Изучаемые вопросы:
· Формулировка стандартной и канонической форм;
· Задача распределения ресурсов;
· Приведение стандартной формы к канонической.
Стандартная задача линейного программирования содержит линейные ограничения в виде неравенств, левые и правые части которых соединены знаком  и формулируется следующим образом.
и формулируется следующим образом.
Найти переменные x 1, x 2,…, xn, которые максимизируют функцию
 (1.1.1)
(1.1.1)
при ограничениях:
 , i=1,2,…,m, (1.1.2)
, i=1,2,…,m, (1.1.2)
 , j = 1, 2,…, n. (1.1.3)
, j = 1, 2,…, n. (1.1.3)
Функцию Z называют целевой функцией, а переменные X = { x 1, x 2 ,…, x n} – планом задачи линейного программирования. Числа c 1 ,c 2,…, cn называются коэффициентами целевой функции Z. Смысл коэффициентов aij перед переменными и правых частей ограничений bi определяется конкретным содержанием задачи. План называется допустимым, если переменные x 1, x 2 ,…, xn удовлетворяют всем ограничениям (1.1.2), (1.1.3), и недопустимым, если хотя бы одно из этих ограничений не выполняется. План X* называется оптимальным, если он допустимый и на нем целевая функция достигает максимального значения.
Примером стандартной задачи линейного программирования (1.1.1)-(1.1.3) может служить задача распределения ресурсов. Допустим, что некоторая фирма производит n видов продукции. Для их производства необходимо m видов ресурсов, максимальные объемы которых ограничены величинами b 1, b 2, …, bm. Считаются заданными и неизменными рыночные цены за единицу продукции c 1, c 2 ,…, cn и нормы затрат aij каждого ресурса i на каждый вид продукции j.
Требуется определить такой план выпуска продукции x 1, x 2 ,…, xn, который максимизирует стоимость ее реализации (выручку). Целевой функцией (1.1.1) является выручка от реализации продукции, а каждое ограничение (1.1.2) означает, что затраты каждого ресурса на производство не превосходят его запаса.
Пример 1.1.1
Для производства двух видов продукции фирма использует два вида ресурсов: ресурс1 – сырье, ресурс2 – время изготовления продукции на оборудовании. Запасы ресурсов ограничены: в день может быть использовано не более 1000 кг сырья и суммарное время работы оборудования не превосходит 25 часов. Нормы затрат каждого ресурса на единицу каждого продукта и рыночные цены заданы в табл. 1.1.1
Таблица 1.1.1
| Ресурс | Нормы затрат на ед. продукции | Запас ресурса | |
| Продукт1 | Продукт2 | ||
| Сырье | a 11 =5 | a 12 =10 | b 1=1000 |
| Время изготовления | a 21 =0,1 | a 22 =0,3 | b 2=25 |
| Цена за ед. продукции | c 1=40 | c 2 =100 |
Требуется найти план выпуска продукции, который обеспечивает максимальную стоимость реализации (выручку).
Обозначим:
x 1 – план выпуска продукции 1,
x 2 – план выпуска продукции 2.
Тогда затраты сырья и времени изготовления, необходимые для производства плана x 1, x 2, будут равны соответственно:
 ,
,
 .
.
План X = { x 1, x 2} будет допустимым, если затраты каждого ресурса не превосходят их запасов, т. е. выполняются неравенства:
 ,
,  .
.
Целевой функцией для данного примера служит общая стоимость реализации плана (выручка) x 1, x 2:  .
.
Таким образом, математически рассматриваемая задача является задачей линейного программирования в стандартной форме:
− найти план выпуска продукции x 1, x 2, который обеспечивают максимальную выручку
 (1.1.4)
(1.1.4)
− при ограничениях:
 , (1.1.5)
, (1.1.5)
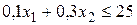 , (1.1.6)
, (1.1.6)
 . (1.1.7)
. (1.1.7)
Каноническая форма. Найти переменные x 1, x 2,…, xn, которые дают экстремум (максимум или минимум) целевой функции (1.1.1)
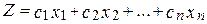
при ограничениях:
 , i = 1, 2,…, m, (1.1.8)
, i = 1, 2,…, m, (1.1.8)
 , j = 1, 2,…, n.
, j = 1, 2,…, n.
Предполагается, что правые части ограничений b i неотрицательны.
Можно показать, что любую задачу линейного программирования можно привести к каноническому виду.
Задача распределения ресурсов может быть приведена к каноническому виду введением в каждое ограничение i дополнительной переменной si, которая означает остаток от производства ресурса i (количество неиспользуемого ресурса). Тогда задача распределения ресурсов состоит в определении значений переменных xj, si, которые максимизируют функцию (1.1.1)

при ограничениях:
 , i = 1, 2,…, m, (1.1.9)
, i = 1, 2,…, m, (1.1.9)
 , j = 1, 2,…, n.
, j = 1, 2,…, n.
Пример 1.1.2
Приведем задачу (1.1.4)-(1.1.7) к канонической форме. Для этого введем две дополнительные переменные:
s 1 – остаток от производства ресурса1 (остаток сырья)
s 2 – остаток от производства ресурса2 (остаток времени изготовления)
Тогда получим каноническую форму задачи:
− найти план x 1, x 2, s 1, s 2, который дает максимальную выручку
 (1.1.10)
(1.1.10)
− при ограничениях:
 , (1.1.11)
, (1.1.11)
 , (1.1.12)
, (1.1.12)
 (1.1.13)
(1.1.13)
Пример 1.1.3
Пусть x 1 = 10 – план выпуска продукции 1, x 2 = 100 – план выпуска продукции 2.
Проверим допустимость плана для задачи (1.1.4)-(1.1.7).
Найдем затраты на производство обоих ресурсов. Для выполнения этого плана потребуется:
 = 5∙10 + 10∙100 = 1050 кг сырья и
= 5∙10 + 10∙100 = 1050 кг сырья и
 = 0,1∙10 + 0,3∙100 = 31 час работы оборудования.
= 0,1∙10 + 0,3∙100 = 31 час работы оборудования.
Такой план выпуска недопустим, т.к. для его выполнения недостаточно ресурсов.
Вопросы для самопроверки
1. Какой план является допустимым в задаче линейного программирования?
2. Какой план является недопустимым в задаче линейного программмиро-вания?
3. Какой план является оптимальным в задаче линейного программиро-вания?
4. Чем отличаются стандартная и каноническая формы задачи линейного программирования?
1.2. Двойственная задача
Изучаемые вопросы:
· Правило построения двойственной задачи;
· Двойственная задача распределения ресурсов;
· Экономический смысл двойственной задачи распределения ресурсов.
Каждой задаче линейного программирования соответствует двойственная задача линейного программирования. Исходная задача называется прямой. Сформулируем правило построения двойственной задачи.
Пусть прямая задача записана в канонической форме: найти переменные x 1, x 2,…, xn, которые максимизируют функцию Z
при ограничениях:
 i = 1, 2,…, m, (1.1.8)
i = 1, 2,…, m, (1.1.8)
 j = 1, 2,…, n. (1.1.3)
j = 1, 2,…, n. (1.1.3)
Тогда по определению двойственная ей задача записывается в виде:
− найти переменные y 1, y 2,…, y m, которые минимизируют функцию W
 (1.2.1)
(1.2.1)
− при ограничениях:
 j =1, 2,…, n (1.2.2)
j =1, 2,…, n (1.2.2)
переменные  i = 1, 2,…, m не имеют ограничения знака.
i = 1, 2,…, m не имеют ограничения знака.
Переменные  i = 1, 2,…, m называются двойственными или теневыми ценами. План двойственной задачи Y = { y 1, y 2, …., y m} называется допус-тимым, если все ограничения двойственной задачи (1.2.2) выполняются.
i = 1, 2,…, m называются двойственными или теневыми ценами. План двойственной задачи Y = { y 1, y 2, …., y m} называется допус-тимым, если все ограничения двойственной задачи (1.2.2) выполняются.
Заметим, что:
- число переменных в двойственной задаче равно числу ограничений в прямой задаче;
- каждому ограничению в прямой задаче соответствует своя двойственная переменная;
- коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи;
- каждой переменной в прямой задаче соответствует ограничение в двойственной задаче. При этом в левую часть данных ограничений входят коэффициенты перед этой переменной в прямой задаче, умноженные на соответствующие двойственные переменные, а правая часть равна коэффициенту целевой функции прямой задачи перед этой переменной.
Замечание. Если прямая задача на минимум целевой функции, то двойственная задача на максимум и в ее ограничениях (1.2.2) знак  нужно заменить на знак
нужно заменить на знак  :
:
− найти переменные y 1, y 2,…, ym, которые максимизируют функцию W:
 (1.2.3)
(1.2.3)
− при ограничениях
 j = 1, 2,…, n (1.2.4)
j = 1, 2,…, n (1.2.4)
переменные  i = 1, 2,…, m не имеют ограничения знака.¡
i = 1, 2,…, m не имеют ограничения знака.¡
Для построения двойственной задачи необходимо привести прямую задачу к каноническому виду и затем записать двойственную ей задачу.
Для задачи распределения ресурсов двойственная задача состоит в определе-нии значений переменных  i = 1, 2,…, m, которые минимизируют функцию
i = 1, 2,…, m, которые минимизируют функцию
 (1.2.1)
(1.2.1)
при ограничениях:
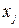 :
:  j = 1, 2,…, n (1.2.2)
j = 1, 2,…, n (1.2.2)
 :
:  i = 1, 2,… m. (1.2.5)
i = 1, 2,… m. (1.2.5)
Ограничение (1.2.5) следует из того, что в (1.1.9) переменная si входит только в одно ограничение.
Выясним экономический смысл двойственной задачи распределения ресурсов. Заметим, что каждое слагаемое в левой части ограничений (1.2.2) должно измеряться в тех же единицах, что правая часть, т.е. денежных единицах. Так как коэффициенты aij означают удельные нормы затрат ресурсов, то каждая двойственная переменная  i = 1, 2,…, m определяет стоимость единицы ресурса i. Отсюда следует, что целевая функция в двойственной задаче
i = 1, 2,…, m определяет стоимость единицы ресурса i. Отсюда следует, что целевая функция в двойственной задаче

определяет стоимость запасов всех ресурсов.
Коэффициенты перед двойственными переменными в левой части двойственных ограничений (1.2.2)
 :
:  j = 1, 2,…, n
j = 1, 2,…, n
задают нормы затрат всех ресурсов, необходимых для производства единицы продукции j. Следовательно, левая часть этих ограничений
 (1.2.6)
(1.2.6)
определяет стоимость ресурсов в теневых ценах, затраченных на производство единицы продукции j (удельные затраты на продукцию j).
Обозначим через 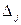 разность между удельными затратами zj и рыночной ценой на продукцию j:
разность между удельными затратами zj и рыночной ценой на продукцию j:
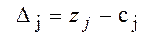 . (1.2.7)
. (1.2.7)
Величину  называют приведенной стоимостью (приведенными издержками) производства продукции j.
называют приведенной стоимостью (приведенными издержками) производства продукции j.
Производство продукции j назовем:
- убыточным, если выполняется неравенство  ;
;
- рентабельным, если выполняется равенство  ;
;
- прибыльным, если выполняется неравенство  .
.
В этих обозначениях ограничения двойственной задачи (1.2.2)
 :
: 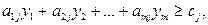 j = 1, 2,…, n
j = 1, 2,…, n
можно теперь записать Δ j ≥ 0.
Отсюда следует, что на допустимых теневых ценах производство всех продуктов неприбыльно.
Тогда двойственную задачу можно записать в виде:
- найти переменные y 1, y 2,…, ym, которые минимизируют функцию (1.2.1)

- при ограничениях
x j: Δj ≥ 0, j = 1, 2,…, n (1.2.8)
 :
:  , i = 1, 2,…, m. (1.2.5)
, i = 1, 2,…, m. (1.2.5)
Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам y 1, y 2, …, ym. Неравенства (1.2.2) означают, что в предлагаемых теневых ценах производство всех видов продукции неприбыльно. При этом (1.2.1) означает, что стоимость приобретаемых ресурсов должна быть минимальна. Таким образом, решение двойственной задачи определяет минимальный уровень теневых цен y 1, y 2, …, ym, при котором производить продукцию неприбыльно.
Пример 1.2.1
Построим двойственную задачу по канонической форме задачи:
- найти план x 1, x 2, s 1, s 2, который дает максимальную выручку
 (1.1.10)
(1.1.10)
- при ограничениях
 , (1.1.11)
, (1.1.11)
 , (1.1.12)
, (1.1.12)
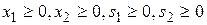 . (1.1.13)
. (1.1.13)
Правило построения двойственной задачи состоит в следующем. Каждому равенству прямой задачи соответствует двойственная переменная. Стрелки в (1.1.11-1.1.12) показывают, что первому равенству соответствует переменная y 1, а второму – переменная y 2.
Для определения целевой функции W двойственные переменные y 1 и y 2 умножаются на правые части равенств (1.1.11), (1.1.12) и складываются:
W = 1000 y 1+ 25 y 2.
Каждой переменной прямой задачи x 1, x 2, s 1, s 2 соответствует одно ограничение двойственной задачи. Левые части этих ограничений для переменной x 1 записываются следующим образом. Двойственные переменные y 1 и y 2 умножаются на коэффициенты перед переменной x 1 в (1.1.11) и (1.1.12) и складываются: 5 y 1+ 0,1 y 2.
Аналогично, записываются левые части ограничений для переменной x 2. Двойственные переменные y 1 и y 2 умножаются на коэффициенты перед переменной x 2 в (1.1.11) и (1.1.12) и складываются: 10 y 1 + 0,3 y 2.
Левая часть ограничений для переменной s 1 равна y 1,а для переменной s 2 – y 2
Правые части ограничений равны коэффициентам целевой функции Z перед переменными x 1, x 2, s 1, s 2. Левые и правые части ограничений соединяются знаком ≥.
В результате двойственная задача имеет вид:
– найти двойственные переменные y 1 и y 2,при которых целевая функция W минимальна
min W = 1000 y 1+25 y 2 (1.2.9)
– при ограничениях  , (1.2.10)
, (1.2.10)
 , (1.2.11)
, (1.2.11)
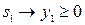 , (1.2.12)
, (1.2.12)
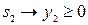 . (1.2.13)
. (1.2.13)
Переменные y 1, y 2, называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям (1.2.10)-(1.2.13).
Переменные y 1, y 2 называются оптимальными, если они допустимые и на них целевая функция W достигает минимума.
Экономически:
- двойственная переменная y 1 определяет теневую цену 1 кг сырья;
- двойственная переменная y 2 определяет теневую цену 1 часа работы оборудования. Тогда
- целевая функция W = 1000 y 1+ 25 y 2 задает стоимость запасов сырья и времени работы оборудования в теневых ценах.
Выражение z 1 = 5 y 1+0,1 y 2 определяет стоимость 5 кг сырья и 0,1 часа времени, затраченных на изготовление единицы продукции 1 в теневых ценах, а выражение z 2 = 10 y 1+ 0,3 y 2 определяет стоимость 10 кг сырья и 0,3 часа времени, затраченных на изготовление единицы продукции 2 в теневых ценах.
Для определения прибыльности производства продукции сравним стоимость ресурсов (в теневых ценах ресурсов), на него затраченных, с выручкой от продажи продукции. Для этого определим приведенные стоимости производства каждого вида продукции
 , (1.2.14)
, (1.2.14)
 . (1.2.15)
. (1.2.15)
Если величина Δ j положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно и выгоднее продать ресурсы по рыночным ценам. Если величина Δ j отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. В этом случае производство прибыльно и выгоднее производить продукцию. Если величина Δ j равны 0, то стоимость ресурсов равна рыночной цене. В этом случае одинаково выгодно продать ресурсы и производить продукцию.
Ограничения двойственной задачи:
 , (1.2.10)
, (1.2.10)
 (1.2.11)
(1.2.11)
можно теперь записать:
Δ1 ≥ 0, (1.2.16)
Δ2 ≥ 0. (1.2.17)
Из последних неравенств следует, что на допустимых теневых ценах производство обоих продуктов неприбыльно. Величины Δ j показывают величину изменения выручки при выпуске единицы этой продукции.
Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам y 1, y 2. Неравенства (1.2.16) и (1.2.17) означают, что в предлагаемых теневых ценах производство обоих видов продукции неприбыльно. При этом (1.2.9) означает, что стоимость приобретаемых ресурсов должна быть минимальна. Таким образом, решение двойственной задачи определяет минимальный уровень рыночных цен y 1, y 2, при котором производить продукцию неприбыльно.
Вопросы для самопроверки
1. Как определяется число переменных в двойственной задаче?
2. Как определяется число ограничений в двойственной задаче?
3. В чем состоит экономический смысл двойственных переменных в задаче распределения ресурсов?
4. В чем состоит экономический смысл целевой функции в задаче распределения ресурсов?
5. В чем состоит экономический смысл двойственных ограничений в задаче распределения ресурсов?
1.3. Базисные решения
Изучаемые вопросы:
· Свободные и базисные переменные;
· Построение двойственных переменных, соответствующих данному базисному решению.
Заметим, что ограничения задачи линейного программирования в канонической форме  i = 1, 2,…, m задают систему m уравнений с n неизвестными. Допустим, что n > m и ранг матрицы этой системы равен m. Среди бесконечного множества решений базисные решения этой системы получаются следующим образом: (n - m) переменных приравняем 0. Эти переменные назовем свободными. Значения остальных переменных получаем из решения системы относительно m остальных переменных. Эти переменные назовем базисными. Базисное решение называется допустимым, если оно неотрицательно.
i = 1, 2,…, m задают систему m уравнений с n неизвестными. Допустим, что n > m и ранг матрицы этой системы равен m. Среди бесконечного множества решений базисные решения этой системы получаются следующим образом: (n - m) переменных приравняем 0. Эти переменные назовем свободными. Значения остальных переменных получаем из решения системы относительно m остальных переменных. Эти переменные назовем базисными. Базисное решение называется допустимым, если оно неотрицательно.
По каждому допустимому базисному решению прямой задачи найдем значения двойственных переменных y 1, y 2, …, ym. Для этого все ограничения двойственной задачи, соответствующие базисным переменным xj, заменим равенствами
 :
:  .
.
Решение полученной системы определяет теневые цены, соответствующие данному базисному решению.
Пример 1.3.1
Запишем систему ограничений прямой задачи
 , (1.1.11)
, (1.1.11)
 (1.1.12)
(1.1.12)
и двойственной задачи
 , (1.2.10)
, (1.2.10)
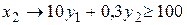 , (1.2.11)
, (1.2.11)
 , (1.2.12)
, (1.2.12)
 . (1.2.13)
. (1.2.13)
1) Пусть x 1, x 2 – свободные переменные (т.е. x 1 = x 2 = 0). Тогда базисные переменные s 1 и s 2 найдем из системы (11),(12) при x 1 = x 2= 0. Отсюда следует, что базисные переменные s 1 = 1000, s 2 = 25.
Таким образом, базисный план имеет вид: x 1 =0, x 2 = 0, s 1 =1 000, s 2 = 25.
Он означает, что продукция не производится. В этом случае выручка составит: Z = 40 x 1 + 100 x 2 = 0
Найдем теперь теневые цены, соответствующие этому базисному решению.
Все ограничения двойственной задачи, соответствующие базисным переменным s1, s2 заменим равенствами, т.е.
 , (1.2.10)
, (1.2.10)
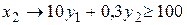 , (1.2.11)
, (1.2.11)
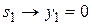 , (1.2.12)
, (1.2.12)
 . (1.2.13)
. (1.2.13)
Отсюда следует, что y 1 =0, y 2 =0. Найдем величины:
D1 = 5 y 1 + 0,1 y 2 – 40 = -40,
D2 = 10 y 1 + 0,3 y 2 - 100 = -100,
т.е. оба производства прибыльны: единица первого продукта увеличивает выручку на 40, а второго – на 100.
2) Пусть s 1, s 2 – свободные переменные (т.е. s 1 = s 2 = 0). Тогда базисные переменные x 1 и x 2 найдем из системы
5 x 1 + 10 x 2 = 1000,
0,1 x 1 + 0,3 x 2 = 25.
Отсюда следует, что базисные переменные x 1 = 100, x 2 = 50. Таким образом, базисное решение имеет вид: x 1 = 100, x 2 = 50, s 1 = 0, s 2 = 0.
Найдем теперь теневые цены, соответствующие этому базисному решению. Все ограничения двойственной задачи, соответствующие базисным перемен-ным x 1, x 2, заменим равенствами, т.е.
 , (1.2.10)
, (1.2.10)
 , (1.2.11)
, (1.2.11)
 , (1.2.12)
, (1.2.12)
 . (1.2.13)
. (1.2.13)
Отсюда следует, что y 1 =4, y2 = 200. Значения приведенных затрат D1 = 0, D2 = 0, т.е. оба производства рентабельные. Двойственные переменные y 1 = 4, y 2 = 200 являются допустимым решением двойственной задачи. Заметим, что решение прямой задачи x 1 = 100, x 2 = 50, s 1=0, s 2=0.
и решение двойственной задачи y 1 =4, y 2 = 200 являются допустимыми решениями. Значения целевых функций равны:
Z =40∙100 + 100∙50 = 9000, W =1000∙4 + 25∙200=9000.
Вопросы для самопроверки
1. Какие переменные называются свободными?
2. Какие переменные называются базисными?
3. Какое базисное решение является допустимым?
Поиск по сайту: