АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение задачи потребительского выбора

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Решение логических задач средствами алгебры логики
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.5.3. Подготовка данных для задачи линейного программирования
  12. I.5.4. Решение задачи линейного программирования

Потребитель стремится максимизировать свою полезность и единственное, что его сдерживает, – это ограниченность дохода. Поэтому модель поведения потребителя можно сформулировать как оптимизационную задачу:

найти такой потребительский набор на котором достигается максимум функции полезности

u (x 1, x 2)

при ограничениях

,

х 1 ³ 0, х 2 ³ 0.

Оптимальное решение этой задачи называется спросом потребителя или точкой локального рыночного равновесия.

Для решения этой задачи нелинейного программирования составим функцию Лагранжа

,

где λ – множитель Лагранжа. Выпишем необходимые и достаточные условия экстремума функции Лагранжа

 

→ (6.3.3)

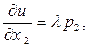→ (6.3.4)

→ (6.3.5)

.

Поделив уравнение (6.3.3) на (6.3.4), получаем систему уравнений для определения спроса :

(6.3.6)

. (6.3.7)

Заметим, что левая часть уравнения (6.3.6) равна предельной норме замены первого товара вторым

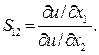
Отсюда следует, что в точке (локального) рыночного равновесия выполняется равенство

, (6.3.8)

т.е. предельная норма замены первого товара вторым равна отношению рыночных цен товаров.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)