Задача на максимум выпуска продукции

Предположим, что фирма производит один вид продукции и технология его производства требует использования двух видов ресурсов. Технологическая связь между затратами ресурсов и выпуском продукции описывается производственной функцией

Обозначим через

p –цену единицы выпускаемой продукции;

w ₁– цену единицы первого ресурса;

w ₂ – цену единицы второго ресурса.

Например, если x_k – число занятых в производстве работников, то w_k – сред-няя заработная плата одного работника. Если x_k – сырье, то w_k – цена единицы сырья. Если x_k – производственные фонды, то w_k – арендная плата за единицу фондов.

Выражение определяет стоимость выпуска продукции, а выражение – – стоимость ресурсов (издержек производства).

Задача максимального выпуска продукции при заданном объеме издержек имеет вид:

– найти объемы ресурсов , которые обеспечивают максимум выпуска продукции

(5.3.1)

– при ограничениях

(5.3.2)

x ₁ ≥ 0, x ₂ ≥ 0(5.3.3)

Величина C определяет верхнее значение стоимости издержек.

Эта задача является задачей нелинейного программирования. Для ее решения построим функцию Лагранжа

(5.3.4)

Если в оптимальном решении должны использоваться все ресурсы x ₁ > 0, x ₂ > 0, то необходимые и достаточные условия оптимальности имеют вид

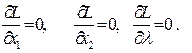(5.3.5)

Отсюда следует, что оптимальное распределение ресурсов и множи-тель Лагранжа λ^* являются решением системы уравнений

(5.3.6)

Заметим, что предельная норма замены первого ресурса вторым равна

Поделив первое уравнение системы уравнений (7.3.6) на второе, получим

(5.3.7)