АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 5.1.1

Читайте также:
  1. I. 1.1. Пример разработки модели задачи технического контроля
  2. IV. ТИПОВОЙ ПРИМЕР РАСЧЕТОВ.
  3. X. примерный перечень вопросов к итоговой аттестации
  4. Б2. Пример №2
  5. Буду на работе с драконом примерно до 21:00.
  6. Булевы функции. Способы задания. Примеры.
  7. В нашем примере каждый доллар первоначального депозита обеспечил 5 дол. средств на банковских счетах.
  8. В некоторых странах, например в США, президента заменяет вице-
  9. В примере
  10. В странах Востока (на примере Индии и Китая)
  11. Вания. Одной из таких областей является, например, регулирова-
  12. Вариационные задачи с подвижными границами. Пример в теории управления.

Обозначим через Y количество единиц продукции, выпускаемое фирмой за день, – x 1количество кг затраченного сырья и x 1– продолжительность изготовления продукции на оборудовании в минутах. Производственная функция затраты-выпуск

определяет выпуск продукции при затратах x 1кг сырья и x 1минут работы оборудования. Коэффициенты 2 и 50 означают, что для производства единицы продукции необходимо 2 кг сырья и 50минут работы оборудования. Эти величины называют нормами затрат ресурсов.

Например, выпуск продукции при затратах 100 кг сырья и 10часах работы оборудования составит

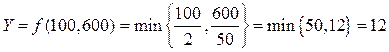
единиц продукции.

Из неравенств (5.1.2) определим минимальное количество ресурсов, необходимое для производства Y=1 2 единиц продукции

,

т.е. требуется не меньше 24 кг сырья и 600 минут работы оборудования.

Мультипликативная производственная функция определяется равенством

, (5.1.3)

где число A определяет шкалу измерения выпуска продукции,параметры

x 1 > 0, x 2 > 0.

В качестве аргументов x 1и x 2мультипликативной функциичасто рассматривают L среднее число работников, занятых в производстве (труд), и Kосновные производственные фонды (капитал). В этом случае мультипликативная функция определяет зависимость выпуска продукции Y от затрат труда L и капитала K по формуле

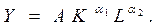
В частности, при x 1=1- x 2 > 0 мультипликативная функция

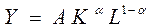(5.1.4)

называется функцией Кобба-Дугласа.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)