 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Анализ оптимальной симплекс-таблицы
Значения во втором столбце определяют значения базисных переменных x 1=100, x 2=50. Все переменные, не входящие в первый столбец, являются свободными и поэтому равны 0: s 1=0, s 2=0.
Таким образом, в оптимальном решении:
- первый продукт производится в количестве 100 единиц (x 1=100);
- второй продукт производится в количестве 50 единиц (x 2 = 50);
- оба ресурса используются в производстве полностью (s 1 = s 2 = 0).
Таким образом, в оптимальном решении прямой задачи
X * = { x 1 = 100, x 2 = 50, s 1 = 0, s 2 = 0}
значения в последней строке симплекс-таблицы определяют соответственно:
- значение целевой функции прямой задачи Z = 9 000 (выручка от реалии-зации продукции составляет 9 000 у.е.);
- значения 0 в столбцах x 1 и x 2 означают, что производства первого и второго продуктов рентабельны: Δ1=0, Δ2=0;
- значение 4 в столбце s 1 означает, что теневая цена 1 кг сырья равна 4 у.е: y 1=4;
- значение 200 в столбце s 2 означает, что теневая цена работы 1 часа оборудования равна 200 у.е.: y 2=200;
- значение целевой функции двойственной задачи:
W = 1 000 y 1 + 25 y 2 = 1 000 ∙4+25∙200 = 9 000 (=Z).
Таким образом, оптимальное решение двойственной задачи:
Y * = { y 1=4, y 2=200, Δ1 =0, Δ2 =0 }.
Вопросы для самопроверки
1. В чем состоит критерий оптимальности?
2. Как определяется ведущая строка?
3. Как заполняется последняя строка симплекс-таблицы?
4. Какой элемент симплекс-таблицы содержит значение выручки?
5. Как находятся значения базисных переменных из симплекс-таблицы?
6. Как находятся значения свободных переменных из симплекс-таблицы?
7. Как находятся значения двойственных переменных из симплекс-таблицы?
2.2. Интервалы устойчивости. Ценность ресурсов
Изучаемые вопросы:
· Свойства оптимальных решений;
· Двойственная переменная как ценность ресурсов;
· Определение оптимального плана;
· Определение границ интервала устойчивости.
Рассмотрим влияние запасов ресурсов на оптимальное решение прямой задачи.
Допустим, что запас ресурса k изменился на величину Δ bk, а запасы осталь-ных ресурсов не изменяются.
Определение. Интервал [ 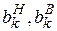 ] называется интервалом устойчивости, если для любого запаса ресурса k из этого интервала выполняются условия:
] называется интервалом устойчивости, если для любого запаса ресурса k из этого интервала выполняются условия:
1) состав оптимальных базисных переменных прямой и двойственной задач не изменяется;
2) оптимальные теневые цены всех ресурсов не изменяются.
Величины  ,
,  называются соответственно максимально допустимым уменьшением и увеличением ресурса k. Таким образом, интервал устойчивости будет равен
называются соответственно максимально допустимым уменьшением и увеличением ресурса k. Таким образом, интервал устойчивости будет равен
 .
.
Изменение запаса ресурса вызывает изменение выручки и оптимального плана выпуска продукции. Из определения интервала устойчивости следует, что структура производственной программы не изменяется при изменении запаса ресурса, т. е. новая производственная программа рекомендует выпускать те же виды продукции, но в других количествах. Математически это означает, что список оптимальных базисных переменных не изменяется при изменении запаса ресурса в интервале устойчивости.
Следующая теорема показывает изменение выручки Z в зависимости от изменения запаса ресурса.
Теорема об оценке. Допустим, что запас ресурса k изменился на величину Δ b k так, что новый запас этого ресурса равен bk + Δ bk, лежит в интервале устойчивости. Тогда выручка изменится на величину
D Z = yk Δ bk.
Если допустимо изменение ресурса на 1, т.е. Δ bk = 1, то из равенства D Z = y k следует, что теневая цена y k показывает изменение выручки D Z, выз-ванное изменением запаса этого ресурса на 1, т.е. определяет ценность этого ресурса для производства. Из теоремы равновесия следует, что теневая цена недефицитного ресурса равна 0. Тогда изменение избыточного ресурса не изменяет величину выручки, т.е. его ценность равна 0.
Найдем изменения оптимального плана, вызванные изменением запаса ресурса k. Заметим, что второй столбец оптимальной симплекс-таблицы определяет объемы производств исходной задачи. Изменение запаса ресурса вызывает изменения в этом столбце по следующему правилу: к их прежним значениям (элементам второго столбца) прибавляются соответствующие элементы столбца переменной xk+n, умноженные на величину изменения запаса ресурса Δ bk. При этом все небазисные переменные остаются равными 0. Максимально допустимые уменьшения и увеличения ресурса и интервал устойчивости можно найти из полученного оптимального плана.
Пример 2.2.1
Из оптимальной симплекс-таблицы исходной задачи можно найти эти изменения, не решая новую задачу симплекс-методом. Далее будут использо-ваться некоторые элементы последней симплекс-таблицы (табл. 2.2.1).
Таблица 2.2.1
| Базис | Значение | x 1 | x 2 | s 1 | s 2 |
| x 1= | 0,6 | -20 | |||
| x 2= | -0,2 | ||||
| z = | |||||
| Δ1 | Δ2 | y 1 | y 2 |
Пусть запас сырья изменяется на величину Δ b 1.
Для определения новых значений базисных переменных нужно к их старым значениям (второй столбец) прибавить соответствующие значения столбца s 1, умноженные на Δ b 1: x 1= 100 + 0,6Δ b 1, x 2= 50 – 0,2Δ b 1.
Значения свободных переменных не изменяются s 1=0, s 2=0. Так как теневая цена этого ресурса y 1 = 4, то выручка изменится на величину D Z = y 1 Δ b 1 = 4 Δ b 1.
Таким образом, при новом запасе сырья оптимальное решение прямой задачи X = { x 1= 100 + 0,6 Δ b 1, x 2 = 50 - 0,2Δ b 1, s 1= 0, s 2 = 0}.
Выручка на этом плане составит Z = 9000 + 4 Δ b 1.
Отсюда следует, что элементы столбца s 1 симплекс-таблицы показывают изменения базисных переменных x 1, x 2 и выручки Z при увеличении первого ресурса на 1: переменная x 1 увеличивается на 0,6, переменная x 2 уменьшается на 0,2 и выручка Z увеличивается на 4.
Поиск по сайту: