Задача на максимум прибыли

Пусть эффект производства определяется разностью между стоимостью выпуска продукции и стоимостью ресурсов (издержек производства)

.

Если величина Z положительна, то производство приносит прибыль, в противном случае – убыток. Будем предполагать, что фирма работает в стабильных условиях и ее поведение определяется стремлением к максимальной прибыли.

В задаче максимальной прибыли требуется найти объемы ресурсов , которые обеспечивают максимальную прибыль

(5.4.1)

при ограничениях

x ₁ ≥ 0, x ₂ ≥ 0.

Это задача нелинейного программирования, для которой функция Лагранжа имеет вид

,

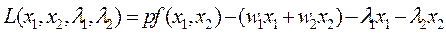где λ _k ≥ 0 – множители Лагранжа.

Если в оптимальном решении должны использоваться все ресурсы, т.е. x ₁ > 0, x ₂ > 0, то необходимые и достаточные условия оптимальности имеют вид

Отсюда следует, что оптимальное распределение ресурсов

является решением системы уравнений

(5.4.2)

Из этой системы уравнений следует

(5.4.3)

т.е. в точке оптимального распределения ресурсов предельная норма замены первого ресурса вторым равна отношению их рыночных цен.

Поиск по сайту: