 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Записать стандартную и каноническую формы
Обозначим:
x 1 – план выпуска продукции 1,
x 2 - план выпуска продукции 2.
Тогда затраты сырья и времени изготовления, необходимые для производства плана x 1, x 2, будут равны соответственно:
5 x 1+10 x 2,
0,1 x 1+0,3 x 2.
План x 1, x 2 будет допустимым, если затраты каждого ресурса не превосходят их запасов т. е. выполняются неравенства:
5 x 1+10 x 2 ≤ 1000,
0,1 x 1+0,3 x 2 ≤ 25.
Целевой функцией служит выручка от реализации допустимого плана x 1, x 2
Z = 40 x 1 + 130 x 2.
Таким образом, математически рассматриваемая задача является задачей линейного программирования в стандартной форме (4.1.1 – 4.1.2):
найти переменные x 1, x 2, которые дают максимум целевой функции Z
max Z = max 40 x 1+130 x 2
при ограничениях
5 x 1 + 10 x 2 ≤ 1000,
0,1 x 1 + 0,3 x 2 ≤ 25,
x 1 ≥ 0, x 2 ≥ 0.
Для канонической формы ограничения (4.1.2) нужно преобразовать в равенства. Для этого введем две дополнительные переменные
s 1 – остаток от производства ресурса 1 (остаток сырья)
s 2 – остаток от производства ресурса 2 (остаток времени).
Тогда получим каноническую форму задачи:
– найти переменные x 1, x 2, s 1, s 2, которые дают максимум целевой функции Z (4.1.3)
max Z = max 40 x 1 + 130 x 2 + 0 s 1+ 0 s 2
– при ограничениях
5 x 1 + 10 x 2 + s 1 =1000,
0,1 x 1 + 0,3 x 2 + s 2 =25.
· Найдем все базисные решения.
Ограничения (4.1.4) образуют систему двух уравнений с четырьмя неизвестными. Среди бесконечного множества решений этой системы базисные решения получаются следующим образом. Две переменных приравняем к 0. Эти переменные назовем свободными. Значения остальных переменных получаем из решения системы. Эти переменные назовем базисными. Базисное решение называется допустимым, если оно неотрицательно.
1) Пусть x 1, x 2 – свободные переменные. Подставляя значения x 1 = 0, x 2 = 0 в (4.1.4), получаем систему уравнений
,
.
Следовательно, базисное решение имеет вид
x 1 = 0, x 2 = 0, s 1 = 1 000, s 2 = 25.
Базисное решение означает, что первой и второй продукт не производится. Это базисное решение является допустимым. Выручка от реализации этого плана составит Z = 40 x 1 + 130 x 2 = 0.
2) Пусть x 1, s 1 – свободные переменные. Подставляя значения x 1 = 0, s 1 = 0 в (4.1.4) получаем систему
,
.
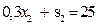Следовательно, базисное решение имеет вид
x 1 = 0, x 2 = 100, s 1 = 0, s 2 = -5.
Это базисное решение означает, что первый продукт не производится, второго продукта производится 100, сырье полностью используется в производстве, для производства не хватает 5 часов работы оборудования. Это базисное решение не является допустимым.
3) Пусть x 1, s 2 - свободные переменные. Подставляя значения x 1=0, s 2=0 в (4.1.4) получаем систему
,
для базисных переменных x 2 и s 1. Следовательно, базисное решение имеет вид
x 1 = 0, x 2 = 250/3 = 83 1/3, s 1 = 166 2/3, s 2 = 0.
Это базисное решение означает, что первый продукт не производится, второго продукта производится 83 1/3, сырье не полностью используется в производстве и его остаток составляет 166 2/3 кг., время работы оборудования полностью используется в производстве. Это базисное решение является допустимым. Выручка от реализации этого плана составит
= 10833 1/3.
4) Пусть x 2, s 1 - свободные переменные. Подставляя значения x 2 = 0, s 1 = 0 в (4.1.4), получаемсистему
.
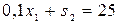для базисных переменных x 1 и s 2. Следовательно, базисное решение имеет вид
x 1=200, x 2= 0, s 1=0, s 2=5.
Базисное решение означает, что первого продукта производится 200, второй продукт не производится, сырье полностью используется в производстве, время обработки не полностью используется в производстве. Это базисное решение является допустимым. Выручка от реализации этого плана составит
= 8000.
5) Пусть x 2, s 2–свободные переменные. Подставляя значения x 2 = 0, s 2 = 0 в (4.1.4), получаем систему
,
.
для базисных переменных x 1 и s 1. Следовательно, базисное решение имеет вид
x 1=250, x 2= 0, s 1 =-250, s 2 =0.
Это базисное решение означает, что первого продукта производится 250, второй продукт не производится, не хватает для производства 250 кг сырья, время работы оборудования используется полностью. Это базисное решение не является допустимым.
6) Пусть s 1, s 2–свободные переменные. Тогда базисные переменные x 1 и x 2найдем из системы уравнений
,
.
Отсюда следует, что базисное решение имеет вид
x 1=100, x 2=50, s 1 =0, s 2 =0.
Это базисное решение означает, что первого продукта производится 100, второго продукта производится 50, сырье и время работы оборудования используется полностью. Это базисное решение является допустимым. Выручка от реализации этого плана составит
Z = 40∙100 + 130∙50 = 10500.
· Определим оптимальное базисное решение
Из теории линейного программирования следует, что оптимальное решение можно найти среди допустимых базисных решений. Отсюда следует, что для определения оптимального решения нужно вычислить значения целевой функции на всех допустимых базисных решениях. Оптимальным будет базисное решение, на котором значение целевой функции наибольшее.
В таблице (4.2.2) приведены все допустимые базисные решения и соответствующие им значения выручки Z.
Таблица 4.4
| № | Базисные переменные | Небазисные переменные | Z | ||
| s 1=1000 | s 2=25 | x 1=0 | x 2=0 | Z=0 | |
| x 2 = 250/3 | s 1 = 166 2/3 | x 1 = 0 | s 2 = 0 | Z= 10833 1/3 | |
| x 1=200 | s 2=5 | x 2= 0 | s 1=0 | Z=8000 | |
| x1=100 | x2=50 | s1 =0 | s2 =0 | Z=10500 |
Максимальное значение выручки достигается на втором базисном решения в этой таблице
X *={ x 1=0, x 2=83 
, s 1 = 166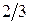 
, s 2 = 0}.
т.е. первый продукт не производится, второй продукт производится в количестве 83 единиц, в производстве не используется 166 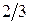кг сырья, в производстве используется все 25 часов (s 2 =0).
Графическое решение задачи
Рассмотрим задачув стандартной форме: найти переменные x 1, x 2,которые обеспечивают максимальное значение функции Z
при ограничениях
,
,
На горизонтальной оси прямоугольной системы координат будем откладывать план выпуска первой продукции x 1, а на вертикальной – план выпуска второй продукции x 2.
Рассмотрим первое ограничение (4.1.5):
.
Множество точек, удовлетворяющих равенству (4.1.6)
,
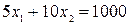образует прямую на плоскости. Построим эту прямую по ее точкам пересечения с осями координат. Для определения координат точки A пересечения с осью 0x 1в уравнение (4.1.6) подставим x2 = 0. Из него следует x 2= 200 т.е. A (200,0). Для определения координат точки B пересечения с осью 0x 2в уравнение (4.1.6) подставим x 1 = 0. Из него следует x 1=100 т.е. B (0,100).
Неравенству (4.1.5) удовлетворяют все точки одной из полуплоскостей, которые образовала построенная прямая. Для ее определения достаточно проверить справедливость неравенства для одной точки. Для начала координат O(0,0) неравенство (4.1.5) выполняется. Следовательно, все точки полу-плоскости, содержащей начало координат, будут графическим изображением этого неравенства. Аналогично построим прямую
по ее точкам пересечения с осями координат: C (250,0), D(0, 83 1/3). Все точки полуплоскости, содержащей начало координат O(0,0), будут графическим изображением неравенства .
Учитывая ограничения на знак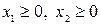 
, множество точек четырехугольника OAMD является множеством всех допустимых решений.
Все угловые точки (крайние точки) четырехугольника OAMD соответствуют допустимым базисным решениям:
угловая точка О(0,0) соответствует базисному решению x 1 = 0, x 2 =0, s 1 = 1 000, s 2 = 25;
угловая точка A(200,0) соответствует базисному решению x 1 = 200, x 2 =0, s 1 = 0, s 2 = 5;
угловая точка M(100,50) соответствует базисному решению x 1 = 100, x 2 = 50, s 1 = 0, s 2 = 0;
угловая точка D(0, 83 1/3) соответствует базисному решению x 1 = 0, x 2 = 83 1/3, s 1 = 166 2/3, s 2 = 0.
Теперь графически найдем точку четырехугольника OAMD, которая определит оптимальное решение.
Из теорем математического анализа следует, что оптимальное решение следует искать только среди точек границы четырехугольника OAMD. Для ее определения в начале координат построим вектор 
, координаты которого являются рыночными ценами. Прямая 
проходит через начало координат перпендикулярно вектору . Она определяет все планы, в которых выручка равна 0. Вектор указывает направление возрастания выручки. Если прямую нулевой выручки (пунктирная линия) перемещать параллельно в направлении вектора 
, то значение выручки будет увеличиваться. Так как среди внутренних точек четырехугольника OAMD оптимального решения не может быть, то прямую нужно переместить до границы четырехугольника OAMD, т. е. до точки D.
Таким образом, точка D определяет оптимальное решение. Соответствующее точке D базисное решение
X *={ x 1=0, x 2=83 , s 1 = 166 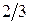, s 2 = 0}
является оптимальным решение. Максимальная выручка будет равна
Z * = 10833 1/3.
Уравнение
определяет уравнение максимальной выручки (верхняя пунктирная линия).
Поиск по сайту: