Пример 5.3.1

Выпуск продукции задается производственной функцией Кобба-Дугласа

,

где Y выпуск продукции, K производственные фонды, L – затраты труда.

Пусть на аренду фондов и оплату труда выделена денежная сумма C = 300 000 рублей, стоимость аренды единицы фондов составляет w_K =1 000 рублей, средняя ставка заработной платы равна w_L = 15 000 рублей. Требуется определить максимальный выпуск.

Решение. Найдем частные производные

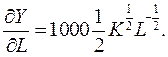
Система уравнений (7.3.6) для оптимальных затрат ресурсов имеет вид

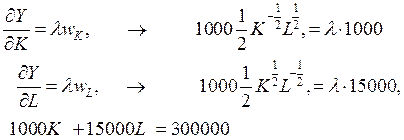
Поделив второе уравнение на первое, получаем, что норма замена основных фондов трудом равна

,

т.е. 15 единиц основных фондов заменяет одного работника

K = 15 L

Из равенства 1 000 K + 15 000 L = 300 000.

Находим

30 000 L = 300 000,

L ^* = 10, K ^* = 150.

Максимальный выпуск продукции равен