 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
II этап: Решение задачи на ЭВМ в среде MS Excel. 1. Формируем диапазон ячеек с исходными данными А1:В4 (см
1. Формируем диапазон ячеек с исходными данными А1:В4 (см. рис. 11).
2. Определяем ячейки, в которых будут содержаться переменные (неизвестные) задачи G2:G4 (см.рис. 11).
На начальном этапе присваиваем неизвестным произвольные значения, например, предполагаем, что вклад в каждый банк составил 1 руб. (см. рис. 11).
Рис.11 Оформление задачи в Excel
3. Вводим формулу в ячейку I7, где будет находиться значение целевой функции (см. рис.12).
4. Вводим зависимости для ограничений (см. рис.12).
5.
Рис.12 Ввод целевой функции и ограничений
Примечание: В ячейках E7:E9 занесены левые части ограничений, а в ячейках G7:G9 – правые части.
Примечание: При вводе формул для целевой функции и ограничений необходимо делать ссылки на ячейки со значениями неизвестных G2:G4, а не на ячейки с именами неизвестных E2:E4.
Примечание: Ограничение (4) и знаки неравенств будут учтены в дальнейшем в окне Поиск решения.
6. Для получения численного решения задачи используем инструмент Поиск решения (Сервис/Поиск решения).
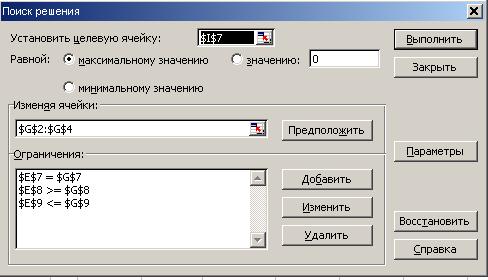
Рис.13 Поиск решения
· Выбор целевой ячейки
В окне Установить целевую ячейку указываем адрес ячейки с целевой функцией I7.
В разделе Равной указать Максимальном значению.
Примечание: Для заполнения окна Установить целевую ячейку необходимо поставить курсор в это окно и на листе выделить ячейку, в которой содержится значение целевой функции.
· Выбор ячеек с переменными
В окно Изменяя ячейки вносим адреса ячеек с неизвестными задачи G2:G4.
Примечание: Для ввода неизвестных можно нажать кнопку Предположить.
Примечание: Для заполнения окна Изменяя ячейки необходимо поставить курсор в это окно и на листе выделить ячейки, в которых содержатся значения переменных.
· Внесение ограничений
Для ввода ограничений необходимо перейти в поле Ограничения и нажать кнопку Добавить. В появившемся диалоговом окне Добавление ограничения, последовательно, для каждого неравенства в разделе Ссылка на ячейку указать адрес ячейки, соответствующей левой части ограничения, а в разделе Ограничения – адрес правой части ограничения.
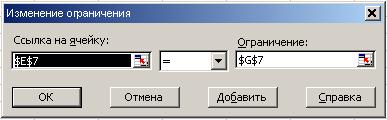
Рис. 14 Ввод ограничения 1
Рис. 15 Ввод ограничения 2
Рис. 16 Ввод ограничения 3
· Параметры модели
Для установки параметров модели необходимо нажать кнопку Параметры и в появившемся диалоговом окне Параметры поиска решения поставить галочки напротив переключателей Линейная модель и Неотрицательные значения (см. рис. 17).
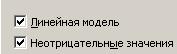
Рис. 17 Параметры поиска решения
Примечание: Полученная модель будет являться линейной, т.к. целевая функция и неравенства для ограничений являются линейными.
· Решение задачи
После ввода всех данных необходимо нажать кнопку Выполнить.
На экране появится диалоговое окно Результаты поиска решения (см. рис. 18). Для отображения решения нужно выбрать переключатель Сохранить найденное решение и в окне Тип отчета выделить строку Устойчивость.
Получение данных по устойчивости требуется для проведения анализа решения задачи.
Рис. 18 Результаты поиска решения
Ответ
В результате решения задачи был получен следующий ответ: В первый банк необходимо вложить 11250 руб., во второй банк – 27500 руб., в третий банк – 11250 руб. 
=(11250,27500,11250).
При этом максимальный годовой доход составит 3781,25 руб.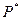 
=3781,25.
Рис. 19 результат решения задачи
Поиск по сайту: