АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Ограничения. Так каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим

Читайте также:
  1. Административно-правовое регулирование отношений в сфере конкуренции и ограничения монополистической деятельности на товарных рынках
  2. Бюджетные ограничения и потребительский выбор.
  3. Бюджетные ограничения кривой безразличия.
  4. Бюджетные ограничения потребителя. Равновесие потребителя. Эффект замещения и дохода
  5. БЮДЖЕТНЫЕ ОГРАНИЧЕНИЯ ПОТРЕБИТЕЛЯ. РАВНОВЕСИЕ ПОТРЕБИТЕЛЯ. ЭФФЕКТ ЗАМЕЩЕНИЯ И ЭФФЕКТ ДОХОДА
  6. Бюджетные ограничения. Бюджетная линия потребителя, её свойства. Наклон бюджетной линии
  7. Великие администраторы добиваются успеха -- не ограничениями и ужесточениями правил. Они представляют -- людям ВОЗМОЖНОСТИ.
  8. Вопрос 5. Какие ресурсные ограничения моделей общей задачи линейного программирования должны анализироваться в первую очередь?
  9. Граждане Республики Беларусь могут иметь в собственности жилые помещения без ограничения их количества и площади
  10. Дадим геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами
  11. Для левой части ограничения 3
  12. ДОБРОВОЛЬНЫЕ ЭКСПОРТНЫЕ ОГРАНИЧЕНИЯ

Так каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим, то на неизвестные 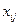накладывается ряд ограничений:

 

Каждый рабочий выполняет только одну операцию

x11+x12+x13=1, (22)

x21+x22+x23=1, (23)

x31+x32+x33=1, (24)

Каждая операция выполняется только одни рабочим

x11+x21+x31=1, (25)

x12+x22+x32=1, (26)

x13+x23+x33=1, (27)

xi –двоичные (28)

Примечание:

Ограничение 7 представляют собой следующие условие:

 

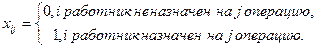
Неизвестные
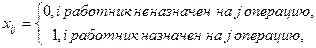i =1,2,3, j = 1,2,3,.
Целевая функция Ограничения
V=10*x11+12*x12+14*x13+ +11*x21+13*x22+14*x23+ +10*x31+9*x32+12*x33 ( мин .) x11+x12+x13=1, x21+x22+x23=1, x31+x32+x33=1, x11+x21+x31=1, x12+x22+x32=1, x13+x23+x33=1, xi –двоичные

Численное решение задачи в Excel аналогично решению транспортной задачи.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)