II. 3.1. Метод отсекающих плоскостей

Этот метод именно и предназначен для решения частного случая задач дискретного программирования – ЦЛП.

Суть метода заключается в следующем. Временно, отбросив условия целочисленности переменных задачи, отыскивается оптимальный план прямым симплекс- методом. Если окажется, что он не удовлетворяет условиям целочисленности, то в задаче формируется дополнительное ограничение, называемое правильнымотсечением, которому заведомо удовлетворяет любое целочисленное решение из ОДР рассматриваемой задачи и не удовлетворяет найденное оптимальное решение.

В общей постановке задача ЦЛП имеет вид[13]:

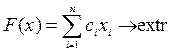
при ограничениях:

.

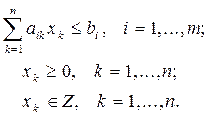Если исходная система ограничений совместна и целевая функция ограничена на множестве решений, тогда можно приступить к отысканию оптимального решения, отбрасывая на первом этапе условие целочисленности решения. Это можно осуществить традиционным симплекс-методом. Допустим, что такое решение получено и оно не удовлетворяет условиям целочисленности. Тогда для й переменной, имеющей нецелочисленное значение, формируется дополнительное ограничение, которое имеет вид

Здесь число есть дробная часть числа

Далее для того, чтобы это ограничение привести к ограничению типа равенства, вводится дополнительная переменная

где Заметим, что введение дополнительной переменной приводит к увеличению размерности базиса пространства переменных рассматриваемой задачи, а как следствие и базисного минора обновленной системы ограничений. Если, полученное выше соотношение переписать в несколько ином виде

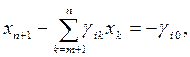
то становится очевидным, что базисная переменная расширяющая базис пространства переменных задачи и есть дополнительная переменная .

Таким образом, в симплекс-таблице формируется дополнительная строка, в которую вписываются величины и , получаемые из последнего соотношения. Отсюда получим некоторый псевдоплан с базисными компонентами и новой составляющей

Важно отметить, что целочисленные точки, а равно и оптимальное целочисленное решение задачи, является внутренней точкой ОДР. Тогда, очевидно, геометрически, получение целочисленного решения, означает движение по линиям уровня целевой функции в направлении, обратном . Поэтому, для дальнейшего решения задачи необходимо применить технику двойственного симплекс-метода.

Таким образом, если после получения оптимального решения двойственным симплекс-методом все компоненты этого решения будет целыми, то задача решена. В противном случае необходимо сформировать еще одно правильное отсечение и так далее, до тех пор, пока решение не будет удовлетворять условиям целочисленности.

Замечание:

· Для того, чтобы иметь право после формирования правильного отсечения пользоваться двойственным симплекс-методом, исходную задачу необходимо привести к задаче на максимум.

· Если на предварительном этапе после применения симплекс-метода без учета условия целочисленности переменных, полученное решение содержит несколько нецелочисленных компонент, то для отсечения выбирается та, которая имеет максимальную дробную часть.

ПРИМЕР: Найти

при условиях

Отбрасывая условия целочисленности, находим оптимальное решение симплекс-методом (см. таблицы I и II)[14]. Получаем оптимальное решение: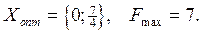

Таблица I.

	Базис
		-1	-4

Таблица II.

	Базис

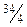
Данное решение не удовлетворяет условиям целочисленности, поэтому необходимо сформировать правильное отсечение. Обе переменные и имеют одинаковые дробные части равные 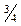. Поэтому отдадим предпочтение истинной переменной и отсечение сформируем для нее.

Теперь запишем правильное отсечение: и, сформировав дополнительную строку, записываем все результаты в таблицу III.

Таблица III.

	Базис
		-		-	-

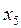
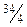
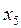
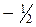
В таблицах IV и V приводятся результаты отыскания плана задачи с помощью двойственного симплекс-метода.

Таблица IV.

	Базис
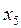
		-3			-5
							-2
	-	-		-	-

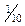
В таблице V представлен новый опорный план, в котором все еще нарушено условие целочисленности.

Таблица V.

	Базис

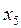
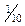
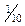
Так как, для истинных переменных задачи 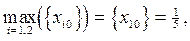то новое правильное отсечение будем формировать по строке :

Запишем правильное отсечение: и, сформировав дополнительную строку, получим таблицу VI.

Таблица VI.

	Базис
	-	-	-			-

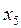
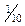
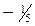
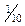
В таблице VII:

Таблица VII.

	Базис
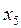
								-2
							-1
								-10

получено искомое целочисленное решение:

Замечание: При формировании правильного отсечения важно помнить, что выбор строки по критерию максимума дробной части осуществляется в первую очередь среди истинных переменных задачи а уж затем по всем остальным не целочисленным переменным. Задача считается решенной, а оптимальное целочисленное решение полученным только в том случае, когда в столбце свободных членов все элементы целые.