 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I.2. Структура оптимизационных задач
Здесь важно отметить, что оптимизационные задачи имеют весьма разнообразные области приложений. Однако, несмотря на это, в целом, их формальное описание имеет общую схему.
Все эти задачи можно классифицировать как задачи поиска экстремума вещественной функции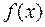 
(здесь 
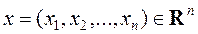), компоненты которой удовлетворяют системе уравнений:
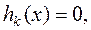(I. 2.1)
набору неравенств:
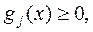(I. 2.2)
а также ограничены сверху и снизу:
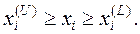
В дальнейшем, функцию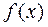 
будем называть целевой функцией, уравнения (1.2.1) – ограничениями типа равенств, неравенства (1.2.2) – ограничениями типа неравенств. Здесь предполагается, что используемые в задаче функциональные зависимости вещественнозначны, а число ограничений конечно.
В общем виде формализованная постановка задачи выглядит так:
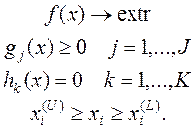(I. 2.3)
Задача носит название задачи условной оптимизации.
Все такие задачи можно классифицировать в соответствии с видом функций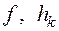 
и 
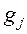, а также с размерностью вектора 
.
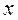Если ограничения (I. 2.1) и (I. 2.2) отсутствуют, а 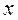представляет собой одномерный вектор, то мы имеем дело с задачами безусловной оптимизации – хотя и простейший, но весьма важный класс оптимизационных задач.
Задачи условной оптимизации, в которых функци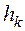и 
и 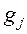являются линейными, носят название задач с линейными ограничениями. В таких задачах сама целевая функция может быть как линейной, так и нелинейной.
Задачи, которые содержат только линейные функции вектора непрерывных переменных 
называются задачами линейного программирования (ЛП)[4].
Существует класс задач с линейными ограничениями и нелинейной целевой функцией. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций:
- 
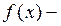квадратичная функция - задача квадратичного программирования;
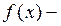- отношение линейных функций – задачи дробно-линейного программирования;
- в задачах динамического программирования целевая функция мультипликативна;
и так далее.
Деление оптимизационных задач на такие классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.
Поиск по сайту: