 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Выбор конструкции смесителя
Московский институт радиотехники, электроники и автоматики
Факультет
Информационные технологии
Лабораторная работа № 2
«Выбор конструкции смесителя методом ЭЛЕКТРА»
По дисциплине
«Методы оптимизации»
Выполнил: студент группы ИТМВ - 01-10 Сорокин А.Б.
Москва 2011 год
Задача данной лабораторной работы: выбрать конструкцию смесителя для системы управления использованием воды в «Умном доме» с использованием метода ЭЛЕКТРА.
Выбор конструкции смесителя.
Сначала составляют таблицу критериев, по которым будут оценивать проекты (см. табл. 1).
Таблица 1
Таблица критериев для оценки проектов
| Критерии | Вес критерия | Шкала | Код | Стремление |
| Интегрирование в систему «умный дом» | хорошее среднее плохое | max | ||
| Расход воды | очень большой большой средний маленький | min | ||
| Контакт пользователя со смесителем | много контактов мало контактов нет контактов | min | ||
| Вандалоустойчивость | большая средняя маленькая | max | ||
| Стоимость смесителя | до 2 тыс. руб. 2 – 3 тыс. руб. 3 – 7 тыс. руб. 7 – 15 тыс. руб. 15 – 30 тыс. руб. | min | ||
| Регулировка температуры | есть нет | max |
Далее составляем таблицу оценок проектов (смесителей). Для 5-ти смесителей заполняем таблицу 2.
Таблица 2
Таблица оценок проектов по критериям.
| Значение критерия | ||||||
| Интегрир. | Расход воды | Контакт | Вандалоуст. | Стоимость | Регулир. темпер. | |
| Вес | ||||||
| Стремление | max | min | min | max | min | max |
1 - смеситель с раздельными кранами;
2 - смеситель однорычажный;
3 - смеситель со встроенным термостатом (с механической регулировкой температуры и напора);
4 - бесконтактный (электронный) смеситель и термостат (с постоянной температурой и напором);
5 - электронный сенсорный смеситель;
6 – английский вариант для одного человека;
7 - смеситель со встроенным термостатом (с механической регулировкой температуры);
Рассматриваем все пары проектов i и j. Если по какому-либо критерию i-ый проект лучше, чем j-ый, то соответствующий критерию вес прибавляется к Pij (эти баллы символизируют выбор «За»), в противном случае — к Nij (эти баллы символизируют выбор «Против»). То же самое справедливо для j-го проекта: если j-ый проект оказывается лучше, чем i-ый, то соответствующий критерию вес прибавляется к Pji, в противном случае — к Nji (обратите внимание на порядок следования индексов j и i у P и N). Если повстречалось одинаковое для i-го и для j-го проектов значение критерия, то оно пропускается. Затем, когда по паре i и j рассмотрены все критерии, находятся отношения Dij = Pij/Nij и Dji = Pji/Nji. Значения D ≤ 1 отбрасываются. Заметим, что Dji = 1/Dij (и наоборот), таким образом, вычисления можно несколько упростить.
Рассмотрим проекты 1 и 2 (i = 1, j = 2):
· по критерию «Интегрирование» (вес критерия 5 баллов - max) проекты 1 и 2 одинаковы, поэтому ничего не делаем;
· по критерию «Расход воды» (вес критерия 5 баллов - min) проект 1 хуже проекта 2;
· по критерию «Контакт» (вес критерия 4 балла - min) проекты 1 и 2 одинаковы, поэтому ничего не делаем.
· по критерию «Вандалоустойчивость» (вес критерия 4 балла - max) проекты 1 и 2 одинаковы, поэтому ничего не делаем.
· по критерию «Стоимость» (вес критерия 3 балла - min) проекты 1 лучше проекта 2.
· по критерию «Регулировка температуры» (вес критерия 2 баллов - max) проекты 1 и 2 одинаковы, поэтому ничего не делаем;
Таким образом, имеем:
P12 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N12 = 0 + 5 + 0 + 0 + 0 + 0 = 5;
D12 =P12/N12 =3/5 = 0,6 < 1 — отбрасываем;
P21 = 0 + 5 + 0 + 0 + 0 + 0 = 5;
N21 = 0 + 0 + 3 + 0 + 3 + 0 = 3;
D21 =P21/N21 =5/3 = 1,67 > 1 — принимаем.
Рассмотрим проекты 1 и 3 (i = 1, j = 3):
P13 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N13 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
D13 =P13/N13 =3/14 = 0,2 < 1 — отбрасываем;
P31 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
N31 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D31 =P31/N31 =14/3 = 4,7 > 1 — принимаем.
Рассмотрим проекты 1 и 4 (i = 1, j = 4):
P14 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
N14 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D14 =P14/N14 =5/18 = 0,27 < 1 — отбрасываем;
P41 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N41 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
D41 =P41/N41 =18/5 = 3,6 > 1 — принимаем.
Рассмотрим проекты 1 и 5 (i = 1, j = 5):
P15 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N15 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D15 =P15/N15 =3/18 = 0,17 < 1 — отбрасываем;
P51 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N51 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D51 =P51/N51 =18/3 = 6 > 1 — принимаем.
Рассмотрим проекты 1 и 6 (i = 1, j = 6):
P16 = 0 + 0 + 0 + 0 + 0 + 0 = 0;
N16 = 0 + 0 + 0 + 0 + 0 + 2 = 2;
D16 =P16/N16 =0/2 = ∞ — принимаем;
P61 = 0 + 0 + 0 + 0 + 0 + 2 = 2;
N61 = 0 + 0 + 0 + 0 + 0 + 0 = 0;
D61 =P61/N61 =2/0 – делить нельзя — отбрасываем.
Рассмотрим проекты 1 и 6 (i = 1, j = 7):
P17 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N17 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
D17 =P17/N17 =3/15 = 0,2 < 1 — отбрасываем;
P71 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
N71 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D71 =P71/N71 =14/3 = 4,7 > 1 — принимаем.
Рассмотрим проекты 2 и 3 (i = 2, j = 3):
P23 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N23 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
D23 =P23/N23 =3/14 = 0,2 < 1 — отбрасываем;
P32 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
N32 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D32 =P32/N32 =14/3 = 4,7 > 1 — принимаем.
Рассмотрим проекты 2 и 4 (i = 2, j = 4):
P24 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
N24 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D24 =P24/N24 =5/18 = 0,28 < 1 — отбрасываем;
P42 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N42 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
D42 =P42/N42 =18/5 = 3,6 > 1 — принимаем.
Рассмотрим проекты 2 и 5 (i = 2, j = 5):
P25 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N25 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D25 =P25/N25 =3/18 = 0,17 < 1 — отбрасываем;
P52 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N52 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D52 =P52/N52 =18/3 = 6 > 1 — принимаем.
Рассмотрим проекты 2 и 6 (i = 2, j = 6):
P26 = 0 + 5 + 0 + 0 + 0 + 2 = 7;
N26 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D26 =P26/N26 =7/3 = 2,3 > 1 — принимаем;
P62 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N62 = 0 + 5 + 0 + 0 + 0 + 2 = 7;
D62 =P62/N62 =3/7 = 0,43 < 1 — отбрасываем.
Рассмотрим проекты 2 и 7 (i = 2, j = 7):
P27 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N27 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
D27 =P27/N27 =3/14 = 0,2 < 1 — отбрасываем;
P72 = 5 + 5 + 4 + 0 + 0 + 0 = 14;
N72 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D72 =P72/N72 =14/3 = 4,7 > 1 — принимаем.
Рассмотрим проекты 3 и 4 (i = 3, j = 4):
P34 = 0 + 0 + 0 + 0 + 3 +2 = 5;
N34 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D34 =P34/N34 =5/18 = 0,27 < 1 — отбрасываем;
P43 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N43 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
D43 =P43/N43 =18/5 = 3,6 > 1 — принимаем.
Рассмотрим проекты 3 и 5 (i = 3, j = 5):
P35 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N35 = 5 + 5 + 0 + 4 + 0 +0 = 14;
D35 =P35/N35 =3/14 = 0,2 < 1 — отбрасываем;
P53 = 5 + 5 + 0 + 4 + 0 = 14;
N53 = 0 + 0 + 0 + 0 + 3 = 3;
D53 =P53/N53 =14/3 = 4,7 > 1 — принимаем.
Рассмотрим проекты 3 и 6 (i = 3, j = 6):
P36 = 5 + 5 + 4 + 0 + 0 + 2 = 16;
N36 = 0 + 0 + 0 + 0 + 3 +0 = 3;
D36 =P36/N36 =16/3 = 5,3 > 1 — принимаем;
P63 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N63 = 5 + 5 + 4 + 0 + 0 + 2 = 16;
D63 =P63/N63 =3/16 = 0,18 < 1 — отбрасываем.
Рассмотрим проекты 3 и 7 (i = 3, j = 7):
P37 = 0 + 0 + 0 + 0 + 0 + 0 = 0;
N37 = 0 + 0 + 0 + 0 + 0 +0 = 0;
D37 =P37/N37 =0/0 = 0 < 1 — отбрасываем;
Тогда.
D73 = 0 < 1 — отбрасываем.
Заметим проекты 3 и 7 одинаковы для данных критериев.
Рассмотрим проекты 4 и 5 (i = 4, j = 5):
P45 = 0 + 0 + 4 + 4 + 3 + 0= 11;
N45 = 0 + 0 + 0 + 0 + 0 + 2 = 2;
D45 =P45/N45 =11/2 = 5,5 > 1 — принимаем;
P54 = 0 + 0 + 0 + 0 + 0 + 2 = 2;
N54 = 0 + 0 + 4 + 4 + 3 + 0 = 11;
D54 =P54/N54 =2/11 = 0,18 < 1 — отбрасываем.
Рассмотрим проекты 4 и 6 (i = 4, j = 6):
P46 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N46 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D46 =P46/N46 =18/3 = 6 > 1 — принимаем;
P64 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N64 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D64 =P64/N64 =2/11 = 0,6 < 1 — отбрасываем.
Рассмотрим проекты 4 и 7 (i = 4, j = 7):
P47 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
N47 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
D47 =P47/N47 =18/5 = 3,6 > 1 — принимаем;
P74 = 0 + 0 + 0 + 0 + 3 + 2 = 5;
N74 = 5 + 5 + 4 + 4 + 0 + 0 = 18;
D74 =P74/N74 =3/18 = 0,27 < 1 — отбрасываем.
Рассмотрим проекты 5 и 6 (i = 5, j = 6):
P56 = 5 + 5 + 4 + 4 + 0 + 2 = 20;
N56 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D56 =P56/N56 =20/3 = 6,7 > 1 — принимаем;
P65 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N65 = 5 + 5 + 4 + 4 + 0 + 2 = 20;
D65 =P65/N65 =3/20 = 0,15 < 1 — отбрасываем.
Рассмотрим проекты 5 и 7 (i = 5, j = 7):
P57 = 5 + 5 + 0 + 4 + 0 + 0 = 14;
N57 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D57 =P57/N57 =14/3 = 4,7 > 1 — принимаем;
P75 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N75 = 5 + 5 + 0 + 4 + 0 + 0 = 14;
D75 =P75/N75 =3/14 = 0,2 < 1 — отбрасываем.
Рассмотрим проекты 6 и 7 (i = 6, j = 7):
P67 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
N67 = 5 + 5 + 4 + 0 + 0 + 2 = 16;
D67 =P67/N67 =3/16 = 0,18 < 1 — отбрасываем;
P76 = 5 + 5 + 4 + 0 + 0 + 2 = 16;
N76 = 0 + 0 + 0 + 0 + 3 + 0 = 3;
D76 =P76/N76 =16/3 = 5,3 > 1 — принимаем.
Составляем матрицу, внося вычисленные (и принятые) значения D. Матрица имеет смысл предпочтений проектов между собой. Для нашего примера матрица выглядит следующим образом (см. табл. 3).
Таблица 3
Полная матрица предпочтений проектов, составленная методом Электра».
| х | –– | –– | –– | –– | ∞ | –– | |
| 4,7 | х | –– | –– | –– | 2,3 | –– | |
| 4,7 | 4,7 | х | –– | –– | 5,3 | –– | |
| 3,6 | 3,6 | 3,6 | х | 5,5 | 3,6 | ||
| 4,7 | –– | х | 6,7 | 4,7 | |||
| –– | –– | –– | –– | –– | х | –– | |
| 4,7 | 4,7 | –– | –– | –– | 5,3 | х |
По матрице строится граф предпочтений (рис. 1).
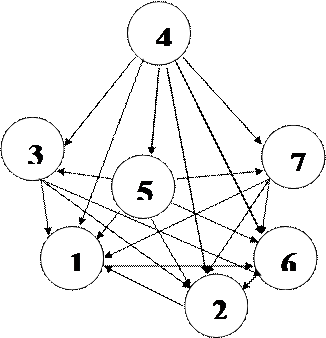 |
Рисунок 1. Вид графа предпочтений.
Из графа, построенного по табл. 3., видно, что проект 4 лучше проектов 1, 2, 3, 5, 6, 7; проект 5 лучше проектов 1, 2, 3, 6, 7; проект 3 лучше проекта 1,2,6; проект 7 равен проекту 3; между проектами 1, 2, 6 образуется петля, трудно определить какой проект лучше. Очевидно, что решение не получено, так как в графе присутствуют петли.
Назначим порог отбора предпочтений C = 3,7 (это соответствует тому, что мы попробуем учесть только более сильные связи в графе, не отвлекаясь на малозначимые расхождения в проектах). Таким образом, матрица разрежается. В ней остаются только самые сильные связи (см. табл. 4).
Таблица 4
Матрица предпочтений проектов, при пороге С=4.
| х | –– | –– | –– | –– | ∞ | –– | |
| 4,7 | х | –– | –– | –– | –– | –– | |
| 4,7 | 4,7 | х | –– | –– | 5,3 | –– | |
| –– | –– | –– | х | 5,5 | –– | ||
| 4,7 | –– | х | 6,7 | 4,7 | |||
| –– | –– | –– | –– | –– | х | –– | |
| 4,7 | 4,7 | –– | –– | –– | 5,3 | х |
Снова строим граф.
 |
Рисунок 2 Вид графа предпочтений для случая порога принятия решений C = 4.
Петель в графе нет, при этом граф остался целостным.
Вывод.
Решение говорит нам о том, что лучший проект — 4. На втором месте — проект 5, третье и четвертое место делят проекты — 3 и 7, пятое место — проект 2, на шестом месте — проект 3, на седьмом месте — проект 7.
Поиск по сайту: