 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Максимизация прибыли на основе предельного подхода
| Объем продукции, тыс.руб. | Цена, тыс. руб. | Общий доход (выручка), млн руб. | Общие издержки, млн руб. | Прибыль, млн руб. | Предельный ДОХОД, млн руб. | Предельные издержки, млн руб. |
| -210 | - | - | ||||
| -110 | ||||||
| -20 | ||||||
| +60 | ||||||
| +130 | ||||||
| +190 | ||||||
| +225 | ||||||
| +230 | ||||||
| +205 | ||||||
| +140 | ||||||
| +45 |
Согласно данным табл. 21.8, самый выгодный объем производства — при 7 тыс. ед. Затем предельные издержки уже превосходят предельный доход, что явно неблагоприятно для предприятия. Следовательно, до 7 тыс. ед. предприятию выгодно производить продукцию, но сверх этой величины производство неэффективно.
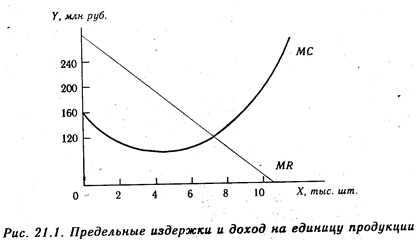
Этот же результат можно получить и графическим методом (рис. 21.1). До 7 тыс. ед. кривая предельных издержек ниже кривой предельного дохода и поэтому каждая дополнительная единица выпускаемой продукции увеличивает сумму прибыли. Максимальная прибыль — это точка пересечения кривой предельных издержек с кривой предельного дохода. После этой точки кривая предельных издержек располагается выше кривой предельного дохода, из чего следует, что каждая дополнительная единица продукции уменьшает прибыль и ее производство неэффективно для предприятия.
Сущность статистического метода заключается в том, что на основании массовых данных исследуется зависимость предельного дохода и предельных издержек от объема реализации продукции.
Данные табл. 21.8 позволяют сделать вывод, что зависимость между предельным доходом и количеством реализованной продукции может быть описана уравнением прямой:
MR = а + bх,
где MR - предельный доход на единицу продукции; х - количество продукции в натуральном выражении.
Найдя неизвестные параметры а и b по методу наименьших
квадратов, получаем
MR = 250 - 20х.
Зависимость предельных издержек от объема производства продукции можно описать уравнением параболы:
МС = а + bх + сх2.
В нашем примере оно будет иметь следующий вид:
МС = 163,16 - 22,235 х + 2,159х2.
Зависимость общей суммы издержек от объема продаж получила следующее выражение:
3 = а + bх = 229 + 115 х.
Приравняем предельный доход и предельные издержки и найдем величину оптимального объема производства продукции, который обеспечит максимальную сумму прибыли:
260 - 20х = 163,16 - 22,235х + 2,159х2,
2,159х2 - 2,235х - 96,84 = 0,
Рх = 250х -10х2;
 тыс. шт.
тыс. шт.
Приведенные расчеты показывают, что оптимальный объем производства составляет 7230 ед.
При таком объеме выручка составит:
В = Р х х = 180 х 7,23 = 1300 млн руб.
Издержки производства:
3 = 229 + 115 х 7,23 = 1060 млн руб.
Прибыль:
П = В - 3 = 1300 - 1060 = 240 млн руб.
Следовательно, данному прдприятию можно придерживаться стратегии наращивания объема производства до 7200 ед. при условии, что себестоимость его продукции существенно не повысится в ближайшей перспективе.
Поиск по сайту: