 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Агрегатная форма общего индекса
При территориальных сравнениях за базу принимают данные по какой-либо одной части территории (например, при региональных сопоставлениях внутри России) или итоговый показатель по всей изучаемой территории в целом, как это имеет место в международных сопоставлениях.
При использовании индексов как показателей выполнения плана за базу сравнения принимаются плановые показатели.
В зависимости от содержания и характера индексируемой величины различают индексы количественных (объемных) показателей (например, индекс физического объема реализации) и индексы качественных показателей (например, индексы цен, себестоимости, производительности труда).
Индивидуальный индекс физического объема реализации равен 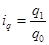 ,
,
q1 – кол-во товара, реализованное в текущем периоде;
q0 – кол-во товара, реализованное в базисном периоде.
Индивидуальный индекс цены рассчитывается как  ,
,
p1 – цена товара в текущем периоде;
p0– цена товара в базисном периоде.
Индивидуальный индекс себестоимости равен  ,
,
z1 – себестоимость продукции в текущем периоде;
z0 – себестоимость продукции в базисном периоде.
Результат расчета индексных отношений может выражаться в коэффициентах или процентах.
Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота: 
Агрегатная форма общего индекса.
Название получили от латинского слова «aggrega», что означает «присоединяю».
При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все элементы.
Достижение в сложных совокупностях сопоставимости разнородных единиц достигается введением соизмерителей. В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цены, количества и др.
Рассмотрим пример с розничными ценами. Цены различных товаров складывать не правомерно, однако, с экономической точки зрения допустимо суммировать товарооборот по этим товарам. Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:

На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен, необходимо количество проданных товаров зафиксировать на каком-то постоянном уровне.
Таким способом получают сводный индекс цен (индекс Г. Пааше). Впервые был предложен немецким ученым Г. Пааше.
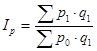
В числителе данного индекса содержится фактический объем товарооборота, в знаменателе условная величина, показывающая каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. При разности числителя и знаменателя данной формулы определяется показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным: 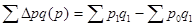 .
.
При другом способе определения агрегатного индекса цен в качестве соизмерителя принимается количество реализованных товаров в базисном периоде q0. Агрегатная форма такого общего индекса имеет вид:

Расчет данного индекса предложен немецким экономистом Э. Ласпейресом.
Применение индексов Пааше и Ласпейреса зависит от цели исследования. Если анализ проводится для определения экономического эффекта от изменения цен в отчетном периоде по сравнению с базисным, то применяется индекс Пааше. Если целью анализа является определение товарооборота при продаже в предстоящем периоде такого же количества товаров, что и в базисном, но по новым ценам, то применяется индекс Ласпейреса.
При синтезировании общего индекса цен вместо фактического товара могут применяться средние величины реализации товаров за два или большее число периодов. При таком способе формула общего индекса имеет вид:

где 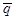 -среднее количество товара, реализованного за анализируемый период.
-среднее количество товара, реализованного за анализируемый период. 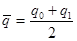
В литературе данный индекс получил название индекс Лоу.
Сводный индекс физического объема реализации характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения.
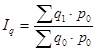
Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.
Или, где весами выступают цены текущего уровня.
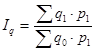
Между рассчитанными индексами существует следующая взаимосвязь:
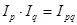
При индексном методе следует учитывать, что факторы, действующие на объем товарооборота (кол-во реализован. товаров) q на их цены p действуют одновременно. При анализе важно определять общий результат их совокупного взаимодействия.
 , где первая скобка- прирост товарооборота за счет фактора цен, вторая - за счет фактора физического объема реализации.
, где первая скобка- прирост товарооборота за счет фактора цен, вторая - за счет фактора физического объема реализации.
Средние индексы
В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (p1q1) и индивидуальными индексами цен  , полученными, например, в результате выборочного наблюдения.
, полученными, например, в результате выборочного наблюдения.
Тогда сводный индекс цен будет выражен в форме средней гармонической:

Если мы имеем данные о стоимости проданной продукции в базисном периоде и индивидуальными индексами цен, то тогда при расчете индекса цен можно использовать формулу средней арифметической взвешенной:

Таким же образом, используя формулы средней гармонической взвешенной и средней арифметической взвешенной можно рассчитать сводные индексы физического объема товарооборота. (см. табл. 11.1)
В средней арифметической форме также может рассчитываться и индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина:

Таблица 11.1
| Индекс | Индивидуальный индекс i | Агрегатный индекс I | Производные индивидуальных индексов | Средний индекс |
| Цен | 
| 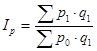
| 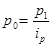
| 
|

| 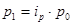
| 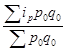
| ||
| Физического объема | 
| 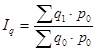
| 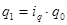
| 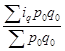
|
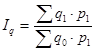
| 
| 
| ||
| Себестоимости | 
| 
| 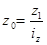
| 
|
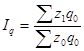
| 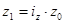
| 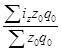
| ||
| Производительности труда | 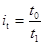
| 
| 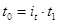
| 
|
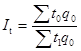
| 
| 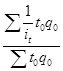
|
Индексы с постоянными и переменными весами
При изучении динамики приходится производить индексные сопоставления более чем за два периода. Поэтому индексы вычисляются как на постоянной, так и на переменной базах сравнения. При этом если сравнение последующих периодов происходит с одним и тем же периодом (начальным), то вычисляются базисные индексы. Но если требуется охарактеризовать последовательное изменение изучаемого явления из периода в период, то вычисляются цепные индексы. Общие индексы в зависимости от их вида (по экономическому содержанию) вычисляются с переменными и постоянными весами-соизмерителями. Рассмотрим систему индексов за «n» периодов.
А. Цепные индексы цен с переменными весами:
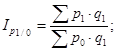
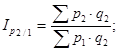


Б. Цепные индексы цен с постоянными весами:
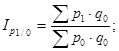

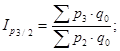

В. Базисные индексы цен с переменными весами:
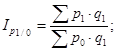

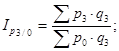

Г. Базисные индексы цен с постоянными весами:

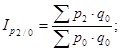

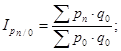
Индексы переменного и постоянного состава
Рассмотрим теперь случай, когда один товар реализуется в нескольких местах или вид продукции производится на ряде предприятий.
Если реализуется только один вид продукции, вполне правомерно рассчитать его среднюю цену в каждом периоде. Индекс переменного состава представляет собой отношение двух полученных средних значений:
При изучении влияния структурных сдвигов применяют индексы, которые находятся во взаимосвязи со средними величинами. Из формулы средней 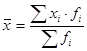 видно, что на ее величину оказывают влияние как значение осредняемого признака xi, так и численность вариантов fi Поэтому при анализе цен важно знать в какой степени это вызвано изменением индексируемой величины (цены), а в какой – количеством реализованной продукции (структурными сдвигами кол-ва реал. продукции. Это выполняется с помощью системы взаимосвязанных индексов:
видно, что на ее величину оказывают влияние как значение осредняемого признака xi, так и численность вариантов fi Поэтому при анализе цен важно знать в какой степени это вызвано изменением индексируемой величины (цены), а в какой – количеством реализованной продукции (структурными сдвигами кол-ва реал. продукции. Это выполняется с помощью системы взаимосвязанных индексов: 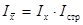 ,
,
где 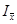 - индекс изменения средней величины;
- индекс изменения средней величины;
 - индекс в неизменной структуре;
- индекс в неизменной структуре;  - индекс, отображающий влияние изменения структуры на динамику средней величины.
- индекс, отображающий влияние изменения структуры на динамику средней величины.
1) При этом: 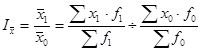 - индекс переменного состава, так как в качестве весов-соизмерителей выступает состав продукции текущего f1 и базисного f0 периодов.
- индекс переменного состава, так как в качестве весов-соизмерителей выступает состав продукции текущего f1 и базисного f0 периодов.
2) 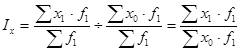 - индекс постоянного состава, так как в качестве весов –соизмерителей выступает состав продукции (товаров) текущего периода f1;
- индекс постоянного состава, так как в качестве весов –соизмерителей выступает состав продукции (товаров) текущего периода f1;
3)  - индекс структурных сдвигов.
- индекс структурных сдвигов.
Применение данных формул рассмотрим на примере данных о продаже товара М в магазинах торговой ассоциации за отчетный период.
Таблица 11.2.
| Магазин | Базисный период | Текущий период | Расчетные графы | ||||
| Цена,1кг, руб. р0 | Количество, кг q0 | Цена,1кг, руб. р1 | Количество, кг q1 | ip | Удельный вес реализации, % | ||
| Базисный период | Отчетный период | ||||||
| 0,96 | 20,0 | 40,0 | |||||
| 0,97 | 40,0 | 30,0 | |||||
| 0,95 | 40,0 | 30,0 | |||||
| Итого | - | - | - | 100,0 | 100,0 |
При анализе изменения уровня цен индексы (гр. 6) показывают, что в текущем периоде было снижение цен на 4% в магазине1, на 3% во втором, 5%-в третьем.
Для определения изменения цен с учетом кол-ва реализованной продукции вычислим индекс цен переменного состава: 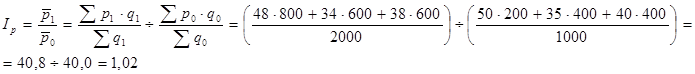
Следовательно, средняя цена реализации данного продукта в трех магазинах в целом возросла в текущем периоде на 2%. Население при покупке каждого килограмма переплачивало 40,8-40,0=0,8 руб. За счет действия каких факторов произошло это повышение? Вычисленные в гр.7 и гр. 8 удельные веса реализации показывают, что с 20 до 40% возрос удельный вес продажи товара А в первом магазине и снизился во втором и третьем магазинах. Как это повлияло на среднюю цену? Для оценки этого фактора определяется индекс влияния структурных сдвигов на изменение средней цены.
 Т.е. структурные сдвиги в реализации объема данной продукции по отдельным магазинам вызвали повышение средней цены в текущем периоде на 6,25%. В абсолютном выражении это вызвало переплату населения на 2,5 руб. (42,5-40,0).
Т.е. структурные сдвиги в реализации объема данной продукции по отдельным магазинам вызвали повышение средней цены в текущем периоде на 6,25%. В абсолютном выражении это вызвало переплату населения на 2,5 руб. (42,5-40,0).
Но в связи с тем, что в текущем периоде в каждом магазине было снижение цен (гр. 4), это также оказало свое влияние на уровень средней цены. 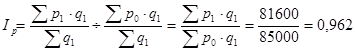
Т.е. в отчетном периоде цены в магазинах снизились в среднем на 0,038 (3,8%). В абсолютном выражении это дало экономию населению при покупке каждого килограмма на 1,7 руб. (81600-86000)/2000=-1,7).
Таким образом проведенный анализ показывает, что рост в текущем периоде средней цены продажи товара А на 2% обусловлен, с одной стороны, ростом на 6,25% в результате структурных сдвигов в объеме реализации и, с другой стороны, снижением в среднем на 3,8% цен. Вычисленные индексы находятся во взаимосвязи:  Данная взаимосвязь удобна тем, что на ее основе по любым двум известным показателям можно определить третий.
Данная взаимосвязь удобна тем, что на ее основе по любым двум известным показателям можно определить третий.
Поиск по сайту: