Параллель векторлар ..... деп аталады. А) коллинеар

64. Бір жазықтықта орналасқан немесе бір

жазықтыққа параллель болатын векторлар.....деп аталады.

65. Кеңістікте векторын базисі бойынша жіктеудің көрінісі:

66. Кеңістіктегі векторының бағыттауыш косинустарын табу формуласы:

67. және векторларының

арасындағы бұрышын анықтау формуласы:

68. базисі бойынша жіктелген

векторы берілген.Осы вектордың аппликатасын көрсетіңіз:

69. векторы үшін бірлік вектордың

абсциссасын көрсету керек:

70. векторы берілген. векторы мен

осі арасындағы бұрыштың косинусы:

71. 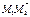векторының координатасын табу керек, егер :

72. векторының модулін табу керек:

73. бірлік векторының координаталарын көрсетіңіз, егер

және нүктелерінің координаталары белгілі болса:

74. векторы берілген. векторыныңи осіне проекциясы:

75. векторының екінші координатасын табыңыз,

егер және бірінші координатасы 6-ға тең болса:

76. векторының және векторлары

бойынша жіктелуінің коэффициентін табу керек:

77. 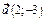векторын және векторлары бойынша жіктеңіз:

78. , векторлары берілген. коэффициентінің

қандай мәнінде және векторлары коллинеар болады:

79. және векторлары берілген.

векторының координатасын анықтау керек:

80. 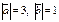векторларының ұзындықтары берілген.

Векторлар арасындағы бұрыш .

Векторлардың скаляр көбейтіндісін табу керек:

81. векторлары берілген.

Ортогональ векторларды көрсетіңіз:

82. Векторлардың векторлық көбейтіндісін табыңыз

:

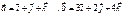83. Векторлардың аралас көбейтіндісін табу керек

:

84. векторларының көбейтіндісі:

85. векторларының көбейтіндісі:

86. векторының координаттарын табыңыз, егер :

87. векторының координаттарын

табыңыз, егер :

88. векторының модулін табыңыз, егер :

89. векторының бағыттауыш косинустарын

табыңыз, егер :

90. векторының базисі бойынша кеңістіктегі

жіктелуі, егер :

91. және векторларының скаляр көбейтіндісін

табу керек, егер :

92. векторының векторына проекциясын табыңыз:

93. шбұрышының ауданын есептеңіз,егер төбелерінің

кооординаталары белгілі болса :

94. 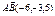және векторларынан

құрылған параллелограммның ауданын табыңыз:

95. шбұрышының ауданын есептеңіз,егер

төбелерінің кооординаталары белгілі болса :

96. Егер мен векторлары ортогональ және

, болса, табу керек :

97. , , 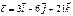векторлары

берілген.Коллинеар векторларды көрсетіңіз.

98. , ,

векторлары берілген. Ортогональ векторларды көрсетіңіз.

99. үшбұрышты пирамидасының көлемін табу керек, егер

, , .

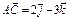100. Параллелепипедтің көлемін табу керек, егер

, ,

101. Бұрыштық коэффициентпен берілген түзудің теңдеуі:

102. теңдеулерімен берілген

түзулердің перпендикулярлық шарты

103. , теңдеулерімен

берілген түзулердің параллельдік шарты

104. және түзулерінің арасындағы

бұрышын анықтайтын формуланы жазу керек:

105. және 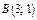екі нүктесі арқылы өтетін

бұрыштық коэффициентпен берілген түзудің теңдеуі:

106. түзуінің бұрыштық коэффициентін анықтау керек:

107. және түзулерінің ара қашықтығын табу керек:

108. Координаттық бұрышты түзуімен

қиып өткенде пайда болған үшбұрыштың ауданын табу керек:

109. ортасынан өтетін перпендикуляр сызықтың

жалпы теңдеуін жазу керек, егер :

110. Кесіндіде екі нүкте берілген және .

Кесіндіні қатынасында бөлетін нүктені табыңыз

111. және нүктелері берілген.

кесіндісін қақ бөлетін нүктенің координаталарын табу керек:

112. нүктесі арқылы өтетін және

түзуіне параллель түзудің теңдеуін құру керек

113. Берілген нүктелері арқылы өтетін түзудің теңдеуі:

114. және нүктелері арқылы түзудің жалпы теңдеуін жазу керек:

115. және түзулері перпендикуляр

болатын -ның мәнін анықтау керек:

116. 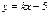және түзулері параллель

болатын -ның мәнін анықтау керек:

117. нүктесінен түзуіне дейінгі ара қашықтықты табу керек:

118. түзуінің нормаль векторының координаталарын анықтау керек:

119. түзуінің бағыттауыш векторының координаталарын анықтау керек:

120. және түзулерінің қиылысу нүктесін табу керек:

121. Эллипстің эксцентриситеті , үлкен жарты осі 5-ке тең.

Фокус арасындағы ара қашықтықты табу керек:

122. шеңбері центрінің координаталарын анықтаңыз:

123. параболасының р параметрінің шамасын анықтаңыз:

124. параболасының р параметрінің шамасын анықтаңыз:

125. гиперболасы фокустарының координаталарын анықтаңыз:

126. эллипсінің эксцентриситетін табыңыз:

127. Гиперболаның остері және . Асимптота теңдеулерін табыңыз:

128. эллипсінің жарты осьтерін табыңыз.

129. Егер гиперболаның нақты осі 6-ға, жорамал

осі 4-ке тең болса,гиперболаның канондық теңдеуін құрыңыз

130. параболасы директрисасының теңдеуін табыңыз.

131. Эллипстің канондық теңдеуінің көрінісі:

132. Эллипстің төбелерінің координаталарын көрсетіңіз:

133. Гиперболаның канондық теңдеуінің көрінісі:

134. Гиперболаның асимптотасының теңдеуі:

135. Эллипстің, гиперболаның эксцентриситетін есептеу формуласы:

136. параболасы директрисасының теңдеуі

137. параболасы фокусының координатасын көрсетіңіз

138. теңдеуінде

және болса, онда бұл теңдеу

139. Егер параболаның симметрия осі - ордината осі болса, онда параболаның теңдеуі:

140. Егер параболаның симметрия осі - абсцисса осі болса, онда параболаның теңдеуі:

141. Кеңістіктегі жазықтықтың жалпы теңдеуін көрсетіңіз:

142. Кеңістіктегі түзудің жалпы теңдеуін көрсетіңіз:

143. Кеңістіктегі нүкте мен нормаль вектор арқылы берілген

жазықтықтың теңдеуін көрсетіңіз:A)

144. 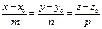түзуі мен

жазықтығының арасындағы 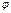бұрышын табу формуласы:

145. Жазықтықтың теңдеуі берілген .

Осы жазықтыққа перпендикуляр векторды табыңыз:

146. Жазықтықтың теңдеуі берілген .

Осы жазықтықтың абсцисса осімен қиылысу нүктелерінің координаттарын табыңыз:

147. нүктесі арқылы өтетін және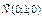

векторына перпендикуляр жазықтықтың жалпы теңдеуі:

148. нүктесі арқылы өтетін және

векторына перпендикуляр жазықтықтың жалпы теңдеуі:

149. Егер жазықтықтың жалпы теңдеуі

түрінде болса, онда кесіндідегі жазықтықтың теңдеуін көрсетіңіз

150. Жалпы теңдеумен берілген түзудің бағыттауыш

векторын табу керек

151. және нүктелері арқылы өтетін

түзудің канондық теңдеуін құру керек:

152. нүктесі арқылы өтетін және

векторына параллель түзудің параметрлік теңдеуін құру керек:

153. және нүктелері арқылы өтетін

түзудің бағыттауыш векторын табыңдар:

154. түзуі мен

жазықтығы арасындағы бұрышын табу керек:

155. 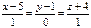түзуі мен

жазықтығы арасындағы бұрышын табу керек:

156. нүктесінен

жазықтығына дейінгі ара қашықтықты табу керек:

157. және нүктелері

арқылы өтетін түзудің кеңістіктегі теңдеуі:

158. нүктесінен

жазықтығына дейінгі ара қашықтықты есептеу формуласы:

159. Кеңістіктегі түзуі мен

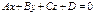жазықтығының параллельдік шарты:

160. Кеңістіктегі түзуі мен

жазықтығының перпендикулярлық шарты:

161. Эллипсоидалды биіктік деп қай жүйедегі теңдеу шешімін айтамыз:

162. Эллипсоидалды биіктік деп қай жүйедегі теңдеу шешімін айтамыз:

163. Мыны теңдеу қалай аталады

164. Мына теңдеу қалай аталады

165. Мына теңдеу қалай аталады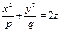

166. Мына теңдеу қалай аталады

167. Конус теңдеуін көрсет:

168. Эллиптикалық цилиндр теңдеуін көрсет:

169. Эллипсоида теңдеуін көрсет:

170. Коніс қатарының жекеше түрін көрсет:

171. Параболоид шешімін тап :

172. Симметрия параболоидасының осьін тап :

173. Гиперболоида симметриясының осьін тап :

174. Гиперболоида симметриясының осьін тап :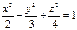

175. Гиперболоида шешімін тап :

176. Гиперболоида қиылысын тап 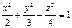осьінде:

177. Эллипсоида қиылысын тап осьінде:

178. Эллипсоида қиылысын тап 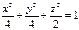мына қатарда :

179. Элипсоида биіктігін тап осьінде:

180. Эллипсоида қиылысын тап мына қатарда :

181. Мына функцияның анықталу облысын тап :

182. Мына функцияның анықталу облысын тап :

183. Мына функцияның анықталу облысын тап :

184. Мына функцияның анықталу облысын тап :

185. функциясы жұп болады егер:

186. функциясы тақ болады егер:

187. Шекті есептеу керек :

188. Екінші тамаша шек неге тең?

189. Шекті есептеу керек :

190. Шекті есептеу керек :

191. Шекті есептеу керек :

192. Шекті есептеу керек :

193. Шекті есептеу керек :

194. Шекті есептеу керек :

195. Шекті анықта

196. Шекті есептеу керек :

197. Шекті есептеу керек :

198. Шекті есептеу керек :

199. Шекті есептеу керек :

200. Шекті есептеу керек :

201. функциясының үзіліс нүктелерін табу керек:

202. функциясының үзіліс нүктелерін табу керек:

203. функциясының үзіліс нүктелерін табу керек:

204. функциясының үзіліс нүктелерін табу керек:

205. функциясының туындысын табыңыз:

206. нүктесіндегі функцияның туындысын тап :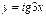

207. нүктесіндегі функцияның туындысын тап :

208. қисығына нүктесі арқылы жүргізілген

жанаманың бұрыштық коэффициентін табу керек

209. функциясының туындысын табыңыз:

210. функциясының туындысы неге тең:

211. функциясының туындысын табыңыз:

212. функциясының туындысын есептеу керек:

213. функциясының дифференциалын көрсетіңіз:

214. функциясының дифференциалын табыңыз:

215. 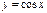функциясының дифференциалын табыңыз:

216. 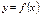функциясы параметрлік түрде берілген

, , мұндағы 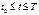, туындысын табу керек:

217. Функция параметрлік түрде берілген

, , туындысын табу керек:

218. функциясының графигіне нүктесінде

жүргізілген жанаманың теңдеуін жазыңыз:

219. Егер 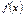функциясы кесіндісінде үзіліссіз және

Поиск по сайту: