 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
При составлении уравнений по второму закону Кирхгофа следует выбирать контура не содержащие источники тока
Общее число уравнений, записываемых по II-му закону Кирхгофа NII определяется как 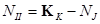 .
.
Число уравнений, записываемых для системы:
 .
.
Полученная система, составленная по I и II законам Кирхгофа решается одним из известных в математике способов, либо с применением ЭВМ.
Если в результате расчетов получены какие-либо из токов отрицательные, то фактическое направление тока в ветви - противоположное.
Метод узловых потенциалов
 Метод базируется на составлении уравнений по I закону Кирхгофа. При этом ток ветви, определенный по закону Ома для ветви заменяется через узловые потенциалы. Узловым напряжением называется напряжение между узлом «k» и произвольно выбранным узлом, потенциал которого искусственно приравнивается нулю (базисный узел). Допустим, имеется схема, изображенная на рисунке, содержащая три узла. Принимаем за базисный узел «3».
Метод базируется на составлении уравнений по I закону Кирхгофа. При этом ток ветви, определенный по закону Ома для ветви заменяется через узловые потенциалы. Узловым напряжением называется напряжение между узлом «k» и произвольно выбранным узлом, потенциал которого искусственно приравнивается нулю (базисный узел). Допустим, имеется схема, изображенная на рисунке, содержащая три узла. Принимаем за базисный узел «3».
Уравнения по I закону Кирхгофа:
 , (1,2)
, (1,2)
Далее записываются токи через закон Ома для участка цепи.
 (3)
(3)
 , (4)
, (4)
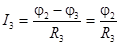 , (5)
, (5)
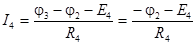 , (6)
, (6)
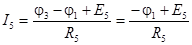 , (7)
, (7)
Заменив сопротивления проводимостями, 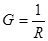 , выполнив подстановку выражений 3, 4, 5, 6, 7 в уравнения 1, 2 и приведя подобные слагаемые, с переносом известных величин вправо, получим следующую систему:
, выполнив подстановку выражений 3, 4, 5, 6, 7 в уравнения 1, 2 и приведя подобные слагаемые, с переносом известных величин вправо, получим следующую систему:

При этом:
 ,
,
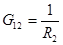 ,
,
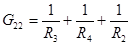 ,
,
Тогда в общем виде система уравнений записывается в виде:

В систему входят следующие величины:
Левая часть
Gkk – собственная проводимость узла (узловая проводимость) – сумма проводимостей ветвей, входящих в узел. В систему уравнений входит со знаком «+».
Gkq -взаимная проводимость ветвей, (сумма проводимостей ветвей непосредственно соединяющая узел k с узлом q), причем эта величина берется со знаком «-».
Правая часть
Правая часть содержит узловые токи (фиктивный ток). Узловой ток определяется суммой (алгебраической) произведений проводимостей ветвей на величину ЭДС, содержащих последнюю и входящих в рассматриваемый узел.
Поиск по сайту: