Замечания

1. При прохождении ЭДС имеет место скачок потенциала.

2. Тангенс угла наклона отрезка, соединяющего две различные точки на потенциальной диаграмме пропорционален току, проходящему через данное сопротивление.

ПРИНЦИП НАЛОЖЕНИЯ. МЕТОД НАЛОЖЕНИЯ

Принцип наложения рассмотрим на примере следующей схемы.

Для заданной схемы запишем уравнения по методу контурных токов.

Обозначим контурные ЭДС.

E₁₁=E₁, E₂₂=- E₃- E₅, E₃₃=E₅-E₆.

Перепишем систему уравнений в виде:

Решая систему линейных уравнений при помощи определителей относительно любого из токов, получим выражение например для тока I_1k.

,

где D - определитель матрицы

,

где

D₁₁,D₁₂, D₁₃ – алгебраические дополнения определителя D, причем D_eq, e=1, получается из D путем вычеркивания е -го столбца и q – строки и умножения последнего на величину (-1)^e+q.

Например, для ,

,

.

Если решать задачу в общем виде, то искомый ток будет определен

.

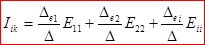Если теперь в полученном выражении тока произвести замену контурных ЭДС алгебраическими суммами ЭДС ветвей, то после группировки слагаемых выражение для контурного тока I_i в виде алгебраических составляющих токов, вызванной каждой из ЭДС ветвей в отдельности.

Это чрезвычайно важной свойство называется принципом наложения и следует из линейности уравнений, описывающих режим цепей с линейными элементами.

Для рассматриваемого примера

.

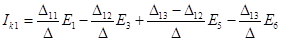т.е. контурный ток I_k1 равен алгебраической сумме составляющих токов, вызванной каждой ЭДС. Кроме того, этот контурный ток равен току в ветви с сопротивлением R₁ и ЭДС E₁.

Метод наложения

На основании принципа наложения на практике расчета эл. цепей широко используется метод наложения.

Результирующая реакция линейной эл. цепи на несколько одновременно приложенных возмущений равна сумме реакций от каждого возмущения в отдельности.

Рассмотрим пример.

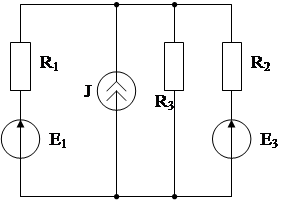Допустим требуется определить ток

I₃=I₃^E1+I₃^E2+I₃^J.

Ток в ветви I₃ определяется возмущениями от трех источников.

Произведем определение реакции на элементе R₃ отдельно от каждого источника возмущения. При этом исключаемые элементы заменяются их внутренними сопротивлениями.

,

.

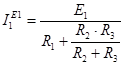
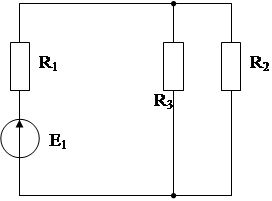При этом E₂ заменяется его внутренним сопротивлением. J заменен внутренним сопротивлением, в рассматриваемом случае g=0, R_вн=¥.

, .

.

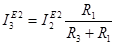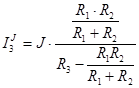БАЛАНС МОЩНОСТИ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ.

Условием баланса любой электрической цепи постоянного тока является равенство нулю суммарной мощности по всем элементам цепи (на основе закона Ломоносова-Лавуазье).

Теорема Теллегена

Сумма произведений напряжений и токов по всем ветвям эл. цепи, удовлетворяющих законам Кирхгофа, равна нулю.

.

,

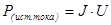. U – напряжение на зажимах источника тока.

.

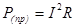Если направление тока и напряжения на источниках энергии совпадают по направлению, то при подсчете мощностей источников мощность берется со знаком «плюс», иначе – «минус». Отрицательная мощность источников энергии говорит от том, что источник работает как потребитель эл. энергии (аккумулятор).

Метод эквивалентного генератора

Эквивалентный Генератор напряжения

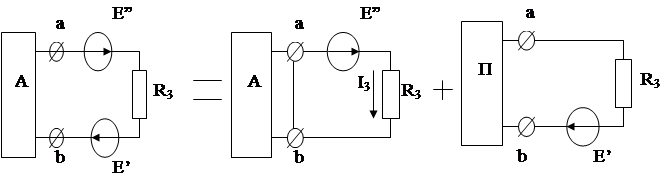
Активный двухполюсник – часть сложной электрической цепи, с источниками энергии и двумя выводами.

Любой активный двухполюсник можно заменить эквивалентным генератором с двумя параметрами: E и R_вн.

Uab – напряжение холостого хода.

Rвн – входное сопротивление активного двухполюсника.

Если E”=E’, то

.

,

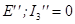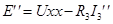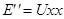
Пассивный двухполюсник можно заменить одним эквивалентным сопротивлением - R_вх.

.

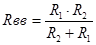Ток в заданной ветви определиться по формуле (теорема Тевенена)

.

Примечание:

Когда в активном двухполюснике убираются источники эл. энергии, то вместо ЭДС ставятся короткозамкнутые перемычки, а ветви, содержащие источники токов обрываются.

ЭКВИВАЛЕНТНЫЙ ГЕНЕРАТОР ТОКА

Напряжение на зажимах исследуемой ветви будет определяться по формуле (теорема Нортона)

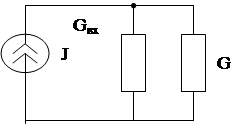
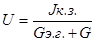
Примечание: Если для схемы Тевенена, в исследуемой ветви находиться отдельный источник ЭДС, то в этом случае ток в ветви определяется по формуле:

.

Если в схеме Нортона вветви присутствует источник тока, то напряджение в этом случае определиться по формуле.

.

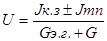
Следует отметить, что обе схемы ЭГ применимы только для расчета токов и напряжений в участке цепи, подключенном к рассматриваемому активному двухполюснику. Для мощностей, развиваемых источниками и для мощностей внутри активного двухполюсника схемы замещения, полученные на основании принципа ЭГ неадекватны.

Метод эквивалентного генератора целесообразен когда требуется определить ток в какой-либо одной ветви или напряжение на одном участке.

МЕТОДИКА РЕШЕНИЯ ЗАДАЧИ ПО МЕТОДУ ЭГ

Э Г Н

1. Выделяется конкретная ветвь «mn», в которой требуется определить ток.

2. Изображается схема с исключенным элементом участка цепи «mn».

3. Определяется входное сопротивление пассивного двухполюсника относительно точек «mn», которое равно внутреннему сопротивлению эквивалентного генератора.

4. Производится расчет схемы с исключенным участком «mn» (режим холостого хода) одним из известных методов расчета для определения ЭДС эквивалентного генератора (напряжения на зажимах «mn»).

5. По формуле Тевенена определяется искомый ток.

Э Г Т

1. Аналогично ЭГН.

2. Аналогично ЭГН

3. Определяется внутренняя проводимость пассивного двухполюсника ЭГТ относительно точек «mn» принципиально обратная величине входного сопротивления.

4. Производиться расчет схемы с закороченным участком «mn» (точки соединены перемычкой), одним из известных методов, для определения тока короткого замыкания источника – ЭГТ.

5. По формуле теоремы Нортона определяется искомое напряжение на участке «mn».

ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Расчет и исследование сложных электрических цепей во многих случаях можно значительно упростить, сделать более наглядными путем преобразования. В результате этих преобразований схемы одного вида преобразуются в схемы другого вида. Целесообразное преобразование эл. цепи приводит к уменьшению ее ветвей или узлов, а следовательно, и числа уравнений, описывающих режим эл. схемы.

1. Последовательное соединение источников ЭДС

В ходе преобразования происходит замена нескольких источников одним.

, .

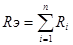2. Параллельное соединение источников тока.

, .

3. Параллельное соединение источников ЭДС и тока

Применяя метод узловых потенциалов,

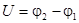, 1 – базисный узел,

.

С другой стороны, ,

по аналогии двух формул,

, .

4. Последовательное соединение источников ЭДС и тока.

Запишем контурные уравнения для тока I

.

С другой стороны

, .

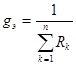5. Свертывание – замена одним элементом (только одного типа).

6. Преобразование «треугольника» в «звезду» и наоборот.

7. Замена источников тока источниками ЭДС и наоборот.

8. Использование теоремы о переносе источников.

8.1 Перенос источников ЭДС.

Применительно к любому узлу электрической цепи, в каждую ветвь можно включить источники ЭДС одинаково направленные относительно узла. На рисунке представлен пример. В ветви 1 ЭДС компенсируются, а в2 и 3 – алгебраически суммируются.

8.2 Перенос источников тока.

В любом замкнутом контуре, параллельно каждой ветви можно включить одинаковый по величине и одинаково ориентированный источник тока.

ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

ОТ ИСТОЧНИКА К ПРИЕМНИКУ

Для исследования передачи энергии от активного двухполюсника к пассивному используем схему:

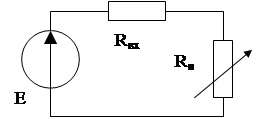R_вх – входное сопротивление источника энергии (активного двухполюсника).

Е=U_хх – эквивалентная ЭДС (постоянная величина).

Rн – входное сопротивление пассивного двухполюсника, которое может принимать любое значение.

Необходимо определить условие выделения максимальной мощности в нагрузке. Мощность в рассматриваемой цепи определяется выражением:

,

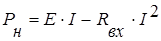где P_н=I²R_н – мощность в нагрузке.

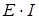- мощность, развиваемая эквивалентным активным двухполюсником.

I²R_вх – мощность потерь в активном двухполюснике.

Для определения тока I, при котором мощность максимальна следует найти производную от Р по I и приравнять ее к нулю.

, откуда .

В общем случае ток в исходной схеме .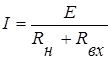

Сопоставив последние два выражения, можно сделать заключение, что при R_н=R_вх мощность, выделяемая в нагрузке максимальна.

Отношение мощности, выделившейся в нагрузке Р_н к мощности Р_а=EI, развиваемой активным двухполюсником, называется к.п.д.

.

Из полученного соотношения следует, что при максимальной мощности пассивного двухполюсника к.п.д. равен 0,5. Более высокие к.п.д. будут при R_н>R_вх. Режим, при котором мощность, выделяемая в нагрузке максимальна называется режимом согласованной нагрузки.

Если в начале линии передачи напряжение U₁ поддерживается постоянным, то линию можно представить в виде последовательного соединения активного двухполюсника с источником ЭДС E_эк=U_хх=U₁ (без внутреннего сопротивления), резистивного элемента, учитывающего сопротивление проводов R_л и пассивного двухполюсника с сопротивлением R.

По выведенным выше формулам определяется мощность на приемнике P₂ и к.п.д. линии передачи:

.

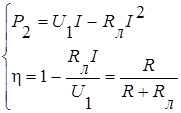Мощность, развиваемая источником P₁=U₁I

Напряжение на выводах приемника: .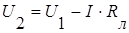

По полученным уравнениям определяются основные характеристики линии: U₂=f(I), P₁=f(I), P₂=f(I), h=f(I).

При R=¥ (холостой ход) ток равен 0 (точка в начале координат)

При R=R_л ток определяется отрезком 0a.

При R=0 – короткое замыкание, ток максимален и равен I_к.

Кроме того, при равенстве R=R_л мощность Р₁ равна удвоенной мощности приемника и h=0,5.

Поиск по сайту: