АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теория свободных электронов в металле. Распределение Ферми – Дирака

Читайте также:
  1. A) эффективное распределение ресурсов
  2. ERG – теория Альдерфера
  3. I. Теория естественного права
  4. I.1.5. Философия как теория и
  5. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  6. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  7. III. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
  8. III. Распределение часов по темам и видам обучения
  9. III. Распределение часов по темам и видам обучения
  10. V. Социологическая теория
  11. А) Теория иерархии потребностей
  12. Административная теория А. Файоля

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физикомЭнрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом кэлектронам в металле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией есть

где

— среднее число частиц в состоянии ,

— энергия состояния ,

— кратность вырождения состояния (число состояний с энергией ),

— химический потенциал (который равен энергии Ферми при абсолютном нуле температуры),

— постоянная Больцмана,

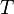— абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур . В этом случае (полагая уровни энергии невырожденными ), функция распределения частиц называется функцией Ферми:

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)