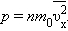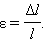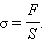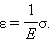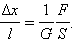|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
Основное уравнение МКТ газов. Температура window.top.document.title = "3.2. Основное уравнение МКТ газов. Температура";
Простейшей моделью молекулярно-кинетической теории является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура).
В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).

|
| Рисунок 3.2.1. Упругое столкновение молекулы со стенкой. |
Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.
Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнуться все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.

|
| Рисунок 3.2.2. Определение числа столкновений молекул с площадкой S. |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно  Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно  По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:

|
Разделив обе части на SΔt, получим:

|
где p – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла (1860 г.). Дж. Максвелл вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.

|
| Рисунок 3.2.3. Распределение молекул по скоростям. T2 > T1. |
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость  где
где  – среднее значение квадрата скорости.
– среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.

|
| Модель. Распределение Максвелла. |
Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с проекциями скоростей υx1, υx2, υx3 и т. д. соответственно. При этом  Каждая группа молекул вносит свой вклад
Каждая группа молекул вносит свой вклад  в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υxi скоростей возникает суммарное давление
в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υxi скоростей возникает суммарное давление

|
Входящая в это выражение сумма – это сумма квадратов проекций υx всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение  квадрата проекции
квадрата проекции  скорости молекул:
скорости молекул:

|
Теперь формулу для давления газа можно записать в виде
|
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:

|
Последнее равенство вытекает из формулы: 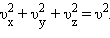
Формула для среднего давления газа на стенку сосуда запишется в виде
|
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости  и средней кинетической энергией
и средней кинетической энергией  поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию  поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то
поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то  (N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению
(N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению  средней кинетической энергии.
средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия  Такой величиной в физике является температура.
Такой величиной в физике является температура.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,

|
Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.

|
| Рисунок 3.2.4. Газовый термометр с постоянным объемом. |
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p0 и p100 на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. Невозможно на опыте получить путем охлаждения газ в состоянии с нулевым давлением, так как при очень низких температурах все газы переходят в жидкие или твердые состояния.

|
| Рисунок 3.2.5. Зависимость давления газа от температуры при V = const. |
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
| TК = TС + 273,15. |
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01° С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда

|
где N – число молекул в сосуде, NA – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
|
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Л. Больцмана (1844–1906 гг.), одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:
| k = 1,38·10–23 Дж/К. |
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
|
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа:
|
В этом соотношении n1, n2, n3, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.

|
| Модель. Полупроницаемая мембрана. |
3.3. Уравнение состояния идеального газа. Изопроцессы window.top.document.title = "3.3. Уравнение состояния идеального газа. Изопроцессы";
Соотношение
| p = nkT, |
связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

|
Здесь N – число молекул в сосуде, NA – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

|
Произведение постоянной Авогадро NA на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:
| R = 8,31 Дж/моль·К. |
Соотношение
| (*) |
называется уравнением состояния идеального газа.
Для одного моля любого газа это соотношение принимает вид:
|
Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный
| V0 = 0,0224 м3/моль = 22,4 дм3/моль. |
Это утверждение называется законом Авогадро.
Для смеси невзаимодействующих газов уравнение состояния принимает вид
|
где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (*) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.
Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.
Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.
Изотермический процесс (T = const)
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:
|

|
| Модель. Изотермический процесс. |
На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.

|
| Рисунок 3.3.1. Семейство изотерм на плоскости (p, V). T3 > T2 > T1. |
Изохорный процесс (V = const)
Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или
|

|
| Модель. Изохорный процесс. |
На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

|
| Рисунок 3.3.2. Семейство изохор на плоскости (p, T). V3 > V2 > V1. |
Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.
Уравнение изохорного процесса может быть записано в виде:
|
где p0 – давление газа при T = T0 = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К–1, называют температурным коэффициентом давления.
Изобарный процесс (p = const)
Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.
Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:
|
где V0 – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К–1. Его называют температурным коэффициентом объемного расширения газов.

|
| Модель. Изобарный процесс. |
На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

|
| Рисунок 3.3.3. Семейство изобар на плоскости (V, T). p3 > p2 > p1. |
Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.
Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.
3.4. Испарение, конденсация, кипение. Насыщенные и ненасыщенные пары window.top.document.title = "3.4. Испарение, конденсация, кипение. Насыщенные и ненасыщенные пары";
Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.
Все реальные газы (кислород, азот, водород и т. д.) при определенных условиях способны превращаться в жидкость. Однако превращение газа в жидкость может происходить только при температурах ниже определенной, так называемой критической температуры Tкр. Например, для воды критическая температура равна 647,3 К, для азота 126 К, для кислорода 154,3 К. При комнатной температуре (≈ 300 К) вода может находиться и в жидком, и в газообразном состояниях, а азот и кислород существуют только в виде газов.
Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно-кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, т. е. к охлаждению жидкости (если нет подвода энергии от окружающих тел).
Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость. В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, когда число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, т. е. когда скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.
Число молекул, вылетающих с единицы площади поверхности жидкости за одну секунду, зависит от температуры жидкости. Число молекул, возвращающихся из пара в жидкость, зависит от концентрации молекул пара и от средней скорости их теплового движения, которая определяется температурой пара.

|
| Модель. Испарение и конденсация. |
Отсюда следует, что для данного вещества концентрация молекул пара при равновесии жидкости и ее пара определяется их равновесной температурой. Установление динамического равновесия между процессами испарения и конденсации при повышении температуры происходит при более высоких концентрациях молекул пара. Так как давление газа (пара) определяется его концентрацией и температурой, то можно сделать вывод: давление насыщенного пара p 0 данного вещества зависит только от его температуры и не зависит от объема. Поэтому изотермы реальных газов на плоскости (p, V) содержат горизонтальные участки, соответствующие двухфазной системе (рис. 3.4.1).

|
| Рисунок 3.4.1. Изотермы реального газа. Область I – жидкость, область II – двухфазная система «жидкость + насыщенный пар», область III – газообразное вещество. K – критическая точка. |
При повышении температуры давление насыщенного пара и его плотность возрастают, а плотность жидкости уменьшается из-за теплового расширения. При температуре, равной критической температуре Tкр для данного вещества, плотности пара и жидкости становятся одинаковыми. При T > Tкр исчезают физические различия между жидкостью и ее насыщенным паром.
Если изотермически сжимать ненасыщенный пар при T < Tкр, то его давление будет возрастать, пока не станет равным давлению насыщенного пара. При дальнейшем уменьшении объема на дне сосуда образуется жидкость и устанавливается динамическое равновесие между жидкостью и ее насыщенным паром. С уменьшением объема все большая часть пара конденсируется, а его давление остается неизменным (горизонтальный участок на изотерме). Когда весь пар превращается в жидкость, давление резко возрастает при дальнейшем уменьшении объема вследствие малой сжимаемости жидкости.
Из газообразного состояния в жидкое можно перейти, минуя двухфазную область. Для этого нужно совершить процесс в обход критической точки K. Один из возможных процессов такого рода показан на рис. 3.4.1 ломаной линией ABC.

|
| Модель. Изотермы реального газа. |
В атмосферном воздухе всегда присутствуют пары воды при некотором парциальном давлении p, которое, как правило, меньше давления насыщенного пара p0. Отношение p / p0, выраженное в процентах, называется относительной влажностью воздуха.

|
Ненасыщенный пар можно теоретически описывать с помощью уравнения состояния идеального газа при обычных для реальных газов ограничениях: давление пара должно быть не слишком велико (практически p ≤ (106–107) Па), а его температура выше некоторого определенного для каждого вещества значения. К насыщенному пару также можно приближенно применять законы идеального газа при условии, что для каждой температуры T давление p0 насыщенного пара определяется по кривой равновесия p0(T) для данного вещества.
Давление p0 насыщенного пара очень быстро возрастает с ростом температуры T. Зависимость p0(T) нельзя получить из законов идеального газа. Давление газа при постоянной концентрации молекул растет прямо пропорционально температуре. В насыщенном паре при повышении температуры возрастает не только средняя кинетическая энергия движения молекул, но и их концентрация. Поэтому давление насыщенного пара при повышении температуры возрастает быстрее, чем давление идеального газа при постоянной концентрации молекул.
Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (т. е. давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.
В частности, при нормальном атмосферном давлении вода кипит при температуре 100 °С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. При подъеме в горы атмосферное давление уменьшается, и поэтому температура кипения воды понижается (приблизительно на 1 °С на каждые 300 метров высоты). На высоте 7 км давление составляет примерно 0,4 атм, и температура кипения понижается до 70 °С.
В герметически закрытом сосуде жидкость кипеть не может, т. к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром. По кривой равновесия p0(T) можно определять температуры кипения жидкости при различных давлениях.
Изображенная на рис. 3.4.1 картина изотерм реального газа описывает процессы испарения и конденсации, т. е. фазовый переход между газообразной и жидкой фазами вещества. На самом деле эта картина является неполной, т. к. из газообразного и жидкого состояний любое вещество может перейти в твердое состояние. При заданной температуре T термодинамическое равновесие между двумя фазами одного и того же вещества возможно лишь при определенном значении давления в системе. Зависимость равновесного давления от температуры называется кривой фазового равновесия. Примером может служить кривая равновесия p0(T) насыщенного пара и жидкости. Если кривые равновесия между различными фазами данного вещества построить на плоскости (p, T), то они разбивают эту плоскость на отдельные области, в которых вещество существует в однородном агрегатном состоянии – твердом, жидком или газообразном (рис. 3.4.2). Изображенные в координатной системе (p, T) кривые равновесия называются фазовой диаграммой.

|
| Рисунок 3.4.2. Типичная фазовая диаграмма вещества. K – критическая точка, T – тройная точка. Область I – твердое тело, область II – жидкость, область III – газообразное вещество. |
Кривая OT, соответствующая равновесию между твердой и газообразной фазами, называется кривой сублимации. Кривая TK равновесия между жидкостью и паром называется кривой испарения, она обрывается в критической точке K. Кривая TM равновесия между твердым телом и жидкостью называется кривой плавления.
Кривые равновесия сходятся в точке T, в которой могут сосуществовать в равновесии все три фазы. Эта точка называется тройной точкой.
Для многих веществ давление pтр в тройной точке меньше 1 атм ≈ 105 Па. Такие вещества при нагревании при атмосферном давлении плавятся. Например, тройная точка воды имеет координаты Tтр = 273,16 К, pтр = 6,02·102 Па. Эта точка используется в качестве опорной для калибровки абсолютной температурной шкалы Кельвина (см. §3.2). Существуют, однако, и такие вещества, у которых pтр превышает 1 атм. Так для углекислоты (CO2) давление pтр = 5,11 атм и температура Tтр = 216,5 К. Поэтому при атмосферном давлении твердая углекислота может существовать только при низкой температуре, а в жидком состоянии при p = 1 атм она вообще не существует. В равновесии со своим паром при атмосферном давлении углекислота находится при температуре 173 К или –80 °С в твердом состоянии. Это широко применяемый «сухой лед», который никогда не плавится, а только испаряется (сублимирует).
3.5. Свойства жидкостей. Поверхностное натяжение window.top.document.title = "3.5. Свойства жидкостей. Поверхностное натяжение";
Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах (см. §3.6), и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком (рис. 3.5.1).

|
| Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед. |
Рис. 3.5.2 иллюстрирует отличие газообразного вещества от жидкости на примере воды. Молекула воды H2O состоит из одного атома кислорода и двух атомов водорода, расположенных под углом 104°. Среднее расстояние между молекулами пара в десятки раз превышает среднее расстояние между молекулами воды. В отличие от рис. 3.5.1, где молекулы воды изображены в виде шариков, рис. 3.5.2 дает представление о структуре молекулы воды.
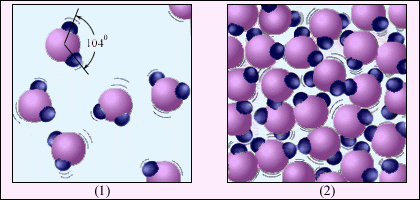
|
| Рисунок 3.5.2. Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз. |
Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.
Жидкости, как и твердые тела, изменяют свой объем при изменении температуры. Для не очень больших интервалов температур относительное изменение объема ΔV / V0 пропорционально изменению температуры ΔT:
|
Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел. У воды, например, при температуре 20 °С βв ≈ 2·10–4 К–1, у стали βст ≈ 3,6·10–5 К–1, у кварцевого стекла βкв ≈ 9·10–6 К–1.
Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρв = 103 кг/м3 вода имеет при температуре 4 °С.
При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому может существовать жизнь в воде замерзающих водоемов.
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместиться с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔAвнеш, пропорциональную изменению ΔS площади поверхности:
| ΔAвнеш = σΔS. |
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2).
Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Ep поверхности жидкости пропорциональна ее площади:
|
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости.
Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 3.5.3).

|
Рисунок 3.5.3.
Подвижная сторона проволочной рамки в равновесии под действием внешней силы 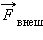 и результирующей сил поверхностного натяжения и результирующей сил поверхностного натяжения  . .
|
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу  Если под действием силы
Если под действием силы  перекладина переместиться на Δx, то будет произведена работа ΔAвнеш = FвнешΔx = ΔEp = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил
перекладина переместиться на Δx, то будет произведена работа ΔAвнеш = FвнешΔx = ΔEp = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил 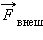 и
и  одинаковы, можно записать:
одинаковы, можно записать:
|
Коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δp. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе 2πR разреза, и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4). Условие равновесия записывается в виде
| σ2πR = ΔpπR2. |
Отсюда избыточное давление внутри капли равно
|

|
| Рисунок 3.5.4. Сечение сферической капли жидкости. |
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности:
|
Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 3.5.5). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании θ = 0, при полном несмачивании θ = 180°.
|
| Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей. |
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.
На рис. 3.5.6 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести  действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fн сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.
действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fн сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.
Отсюда следует:
|

|
| Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре. |
При полном смачивании θ = 0, cos θ = 1. В этом случае
|
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.
3.6. Кристаллические и аморфные тела window.top.document.title = "3.6. Кристаллические и аморфные тела";
По своим физическим свойствам и молекулярной структуре твердые тела разделяются на два класса – аморфные и кристаллические тела.
Характерной особенностью аморфных тел является их изотропность, т. е. независимость всех физических свойств (механических, оптических и т. д.) от направления. Молекулы и атомы в изотропных твердых телах располагаются хаотично, образуя лишь небольшие локальные группы, содержащие несколько частиц (ближний порядок). По своей структуре аморфные тела очень близки к жидкостям (см. §3.5). Примерами аморфных тел могут служить стекло, различные затвердевшие смолы (янтарь), пластики и т. д. Если аморфное тело нагревать, то оно постепенно размягчается, и переход в жидкое состояние занимает значительный интервал температур.
В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl (рис. 3.6.1). Такие кристаллы называются ионными.

|
| Рисунок 3.6.1. Кристаллическая решетка поваренной соли. |
В каждой пространственной решетке можно выделить структурный элемент минимального размера, который называется элементарной ячейкой. Вся кристаллическая решетка может быть построена путем параллельного переноса (трансляции) элементарной ячейки по некоторым направлениям.
Теоретически доказано, что всего может существовать 230 различных пространственных кристаллических структур. Большинство из них (но не все) обнаружены в природе или созданы искусственно.
Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо).
Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.
В отличие от монокристаллов, поликристаллические тела изотропны, т. е. их свойства одинаковы во всех направлениях. Поликристаллическое строение твердого тела можно обнаружить с помощью микроскопа, а иногда оно видно и невооруженным глазом (чугун).
Многие вещества могут существовать в нескольких кристаллических модификациях (фазах), отличающихся физическими свойствами. Это явление называется полиморфизмом. Переход из одной модификации в другую называется полиморфным переходом. Интересным и важным примером полиморфного перехода является превращение графита в алмаз. Этот переход при производстве искусственных алмазов осуществляется при давлениях 60–100 тысяч атмосфер и температурах 1500–2000 К.
Структуры кристаллических решеток экспериментально изучаются с помощью дифракции рентгеновского излучения на монокристаллах или поликристаллических образцах.
На рис. 3.6.2 приведены примеры простых кристаллических решеток. Следует помнить, что частицы в кристаллах плотно упакованы, так что расстояние между их центрами приблизительно равно размеру частиц. В изображении кристаллических решеток указывается только положение центров частиц.

|
| Рисунок 3.6.2. Простые кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка. |
В простой кубической решетке частицы располагаются в вершинах куба. В гранецентрированной решетке частицы располагаются не только в вершинах куба, но и в центрах каждой его грани. Изображенная на рис. 3.6.1 решетка поваренной соли состоит из двух вложенных друг в друга гранецентрированных решеток, состоящих из Na+ и Cl–. В объемноцентрированной кубической решетке дополнительная частица располагается в центре каждой элементарной кубической ячейки.
Кристаллические структуры металлов имеют важную особенность. Положительно заряженные ионы металла, образующие кристаллическую решетку, удерживаются вблизи положений равновесия силами взаимодействия с «газом свободных электронов» (рис. 3.6.3). Электронный газ образуется за счет одного или нескольких электронов, отданных каждым атомом. Свободные электроны способны блуждать по всему объему кристалла.

|
| Рисунок 3.6.3. Структура металлического кристалла. |
3.7. Деформация window.top.document.title = "3.7. Деформация";
В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.
Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.

|
| Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия. |
Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением Δl, возникающим под действием внешней силы  Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).
Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).
Отношение абсолютного удлинения Δl к первоначальной длине l образца называется относительным удлинением или относительной деформацией ε:
|
При растяжении ε > 0, при сжатии ε < 0.
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F > 0 при деформации растяжения и F < 0 – при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
|
За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления.
Зависимость между ε и σ является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси абсцисс откладывается относительное удлинение ε, а по оси ординат – механическое напряжение σ. Типичный пример диаграммы растяжения для металлов (таких как медь или мягкое железо) представлен на рис. 3.7.2.
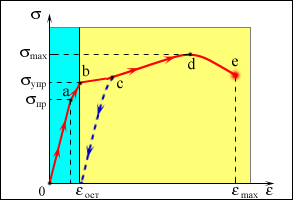
|
| Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций. |
При малых деформациях (обычно существенно меньших 1 %) связь между σ и ε оказывается линейной (участок Oa на диаграмме). При этом при снятии напряжения деформация исчезает. Такая деформация называется упругой. Максимальное значение σ = σпр, при котором сохраняется линейная связь между σ и ε, называется пределом пропорциональности (точка a). На линейном участке выполняется закон Гука:
|
Коэффициент E в этом соотношении называется модулем Юнга.
При дальнейшем увеличении напряжения связь между σ и ε становится нелинейной (участок ab). Однако при снятии напряжения деформация практически полностью исчезает, т. е. восстанавливаются размеры тела. Максимальное напряжение на этом участке называется пределом упругости.
Если σ > σупр, образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация εост. Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение σmax, которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала.
Материалы, у которых диаграмма растяжения имеет вид, показанный на рис. 3.7.2, называются пластичными. У таких материалов обычно деформация εmax, при которой происходит разрушение, в десятки раз превосходит ширину области упругих деформаций. К таким материалам относятся многие металлы.
Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
Аналогичным закономерностям подчиняется и деформация сдвига (рис. 3.7.1 (2)). В этом случае вектор силы  направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением Δx / l, а напряжение – отношением F / S (сила, действующая на единицу площади поверхности). При малых деформациях
направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением Δx / l, а напряжение – отношением F / S (сила, действующая на единицу площади поверхности). При малых деформациях
Поиск по сайту: |
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (2.453 сек.) |