Закон Кулона

Сила взаимодействия заряженых неподвижных тел (или взаемодействие точечных електр. зарядов), размерами которых можно пренебречь по сраснению с расстоянием между ними, прямо пропорциальна значениям их зарядов и обратно пропорциональна квадрату расстояния между ними. F = k (q1 * q2) / r2

3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

- существует вокруг электрического заряда, материально.

Основное свойство электрического поля: действие с силой на эл.заряд, внесенный в него.

Электростатическое поле- поле неподвижного эл.заряда, не меняется со временем.

Напряженность электрического поля. - количественная характеристика эл. поля.

- это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда.

- не зависит от величины внесенного заряда, а характеризует электрическое поле!

Силовые линии эл. поля - непрерывные линии, касательными к которым являются векторы напряженности эл.поля в этих точках.

Однородное эл.поле - напряженность поля одинакова во всех точках этого поля.

Свойства силовых линий: не замкнуты (идут от + заряда к _), непрерывны, не пересекаются,

их густота говорит о напряженности поля (чем гуще линии, тем больше напряженность).

4. Теорема Гаусса (закон Гаусса) -- один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.

Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля.

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.

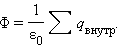
Электростатическое поле шара.

Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью .

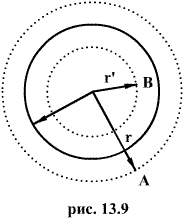
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда 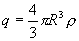, расположенного в центре шара. Тогда вне шара

(13.10)

а на его поверхности (r=R)

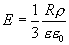
(13.11)

В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен

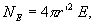
с другой стороны, в соответствии с теоремой Гаусса

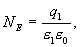
Из сопоставления последних выражений следует

(13.12)

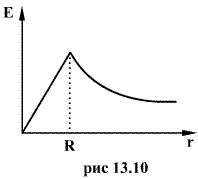
Где 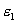- диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)

5. Работа при перемещении заряда в электрическом поле.

На всякий заряд, находящийся в электрическом поле, действует сила, и поэтому при движении заряда в поле совершается определенная работа. Эта работа зависит от напряженности поля в разных точках и от перемещения заряда. Но если заряд описывает замкнутую кривую, т. е. возвращается в исходное положение, то совершаемая при этом работа равна нулю, как бы ни было сложно поле и по какой бы прихотливой кривой ни происходило движение заряда.

Это важное свойство электрического поля нужно несколько пояснить. Для этого рассмотрим сначала движение тела в поле силы тяжести. Работа, как мы знаем (см. том I), равна произведению силы на перемещение и на косинус угла между ними: A=Fs cosa. Если этот угол острый (a<90°), то работа положительна, если же угол тупой (a>90°), то работа отрицательна. В первом случае мы получаем работу за счет действия силы F, во втором — затрачиваем работу на преодоление этой силы. Представим себе, что в поле земного притяжения, т. е. в пространстве вблизи земной поверхности, где действует гравитационная сила притяжения к Земле, перемещается какое-нибудь. тело. Мы предполагаем, что при этом перемещении нет трения, так что тело не испытывает изменений состояния, которые могут сопровождаться изменениями его внутренней энергии: тело не нагревается, не распадается на части, не изменяет своего агрегатного состояния, не испытывает пластической деформации и т. д. В таком случае всякое перемещение тела в поле силы тяжести может сопровождаться лишь изменением потенциальной и кинетической энергии. Если тело опускается, то потенциальная энергия системы Земля — тело уменьшается, а кинетическая энергия тела соответственно увеличивается; наоборот, при подъеме тела происходит возрастание потенциальной энергии и одновременно уменьшение кинетической энергии. При этом полная механическая энергия, т. е. сумма потенциальной и кинетической, остается постоянной (см. том I) Как бы ни был сложен путь тела в поле силы тяжести (подъем и опускание по вертикальной, наклонной или криволинейной траектории, передвижение по горизонтальному направлению), но если в конце концов тело приходит в исходную точку, т. е. описывает замкнутый путь, то система Земля — тело возвращается в исходное положение и имеет ту же самую энергию, какой она обладала до начала перемещения тела. Это означает, что сумма положительных работ, совершенных силой тяжести при опускании тела, равна по модулю сумме отрицательных работ, совершенных силой тяжести на участках пути, соответствующих подъему тела. Поэтому алгебраическая сумма всех работ, совершаемых силой тяжести на отдельных участках пути, т. е. полная работа на замкнутом пути, равна нулю.

Из изложенного ясно, что наш вывод справедлив лишь в том случае, если в процессе участвовала лишь сила тяжести и отсутствовала сила трения и всевозможные другие силы, могущие вызвать указанные выше изменения внутренней энергии. Таким образом, силы гравитационного поля, в отличие от многих других сил, например сил трения, обладают свойством, которое мы можем сформулировать так: работа, совершаемая гравитационными силами при перемещении тела по замкнутому пути, равна нулю. Нетрудно видеть, что это свойство гравитационных сил является выражением закона сохранения (консервации) полной механической энергии. В связи с этим силовые поля, которые обладают указанным свойством, называют консервативными.

6. РАЗНОСТЬ ПОТЕНЦИАЛОВ, (электрическое напряжение), разность в НАПРЯЖЕНИИ (ЭЛЕКТРИЧЕСКОМ ПОТЕНЦИАЛЕ) между двумя точками в цепи или в электрическом поле. Обычно выражается в ВОЛЬТАХ. Равна работе по перемещению единичного электрического заряда из одной точки в другую.

7. Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал 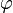связаны соотношением[1]

или обратно[2]:

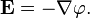
Здесь — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

где 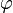— электростатический потенциал (в вольтах), — объёмная плотность заряда (в кулонах на кубический метр), а 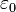— электрическая постоянная (в фарадах на метр).

8. Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):

Wp1 = A10.

(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Эквипотенциальные поверхности — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю или к ньютоновскому гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.

Поверхность проводника в электростатике является эквипотенциальной поверхностью. Кроме того, помещение проводника на эквипотенциальную поверхность не вызывает изменения конфигурации электростатического поля. Этот факт используется в методе изображений, который позволяет рассчитывать электростатическое поле для сложных конфигураций.

В (стационарном) гравитационном поле уровень неподвижной жидкости устанавливается по эквипотенциальной поверхности. В частности, приближенно можно утверждать, что по эквипотенциальной поверхности гравитационного поля Земли проходит уровень океанов[1]. Форма поверхности океанов[2], продолженная на поверхность Земли, называется геоидом и играет важную роль в геодезии. Геоид, таким образом является эквипотенциальной поверхностью силы тяжести, состоящей из гравитационной и центробежной составляющей.

9. Потенциал является важной характеристикой электрического поля, он определяет всевозможные энергетические характеристики процессов, проходящих в электрическом поле. Кроме того, расчет потенциала поля проще расчета напряженности, хотя бы потому, что является скалярной (а не векторной) величиной. Безусловно, что потенциал и напряженность поля связаны между собой достаточно сложными формулами.

ПОПРОБУЕМ ВЫЯСНИТЬ СВЯЗЬ ПРОСТЫМИ СЛОВАМИ:.

Eсли перемещать единичный заряд даже и в неоднородном эл. поле, то энергия на его перемещение и есть потенциал между точками, между которыми его перемещали.

Напряженность - это силовая характеристика эл. поля, а разность потенциалов - энергетическая характеристика эл. поля, поэтому разность потенциалов равна произведению напряженности на перемещение заряда U=E*S

Связь между напряженностью электростатического поля и потенциалом можно выразить с помощью понятия градиента потенциала:

E = - grad Ф (далее математика).

10. Электрический диполь – это система, двух точечных зарядов +q и –q, жестко связанных между собой и смещенных на расстояние l друг относительно друга. Смещение обоих зарядов характеризуют вектором, направленным от отрицательного заряда к положительному. Диполь характеризуется электрическим моментом диполя (рис. 1.17)

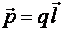
Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей. Главная после суммарного заряда и положения системы в целом (ее радиус-вектора) характеристика конфигурации зарядов системы при наблюдении ее издали.

В однородном электрическом поле электрический диполь просто поворачивается вокруг своего центра масс вдоль силовых линий электрического поля и увеличивает расстояние между своими зарядами (если это возможно по физике системы).

В неоднородном электрическом поле электрический диполь не просто разворачивается, он еще начинает притягиваться в направлении градиента поля, то есть втягиваться в область усиления электрического поля (туда, где силовые линии гуще)

11. Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю:

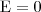
напряженность поля внутри проводника

Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместяться только на поверхности проводника. Это вытекает непосредственно из теоремы Гаусса, согласно которой заряд Q, который находится внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

теорема Гаусса для проводника

поскольку во всех точках внутри замкнутой поверхности D=0.

Теперь мы будем искать взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности σ. Для этого используем теорему Гаусса для бесконечно малого цилиндра с основаниями ΔS, который пересекает границу проводник—диэлектрик. Ось цилиндра направлена вдоль вектора Е (рис. 1). Поток вектора электрического смещения через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводника Е1 (а следовательно, и D1) есть нуль, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Используя теорему Гаусса, этот поток (DΔS) равен сумме зарядов (Q=σΔS), находящихся внутри поверхности: DΔS=σΔS т.е.

вектор электрического смещения для проводника (1)

или

вектор электрического смещения для проводника (2)

где ε — диэлектрическая проницаемость среды, находящаяся вокруг проводника.

Значит, напряженность электростатического поля у поверхности проводника задается поверхностной плотностью зарядов. Можно показать, что формула (2) задает напряженность электростатического поля вблизи поверхности проводника абсолютно произвольной формы.

Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля (рис. 2, а). На одном конце проводника будет собираться избыток положительного заряда, на другом — избыток отрицательного заряда. Эти заряды называются индуцированными (наведенными). Процесс будет продолжаться до тех пор, пока внутри проводника напряженность поля не станет равной нулю, а линии напряженности вне проводника — перпендикулярными его поверхности (рис. 2, б). Значит, нейтральный проводник, который внесен в электростатическое поле, разрывает часть линий напряженности; эти линии напряженности заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности нашего проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.

Из рис. 2, б мы видим, что индуцированные заряды образуются на проводнике вследствие смещения их под действием поля, т. е. σ есть поверхностной плотностью смещенных зарядов. Согласно (1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. По этой причине вектор D получил название вектора электрического смещения.

проводники в электростатическом поле

Поскольку в состоянии равновесия заряды отсутствуют внутри проводника, то создание внутри него полости не окажет влияния на конфигурацию расположения зарядов и тем самым на электростатическое поле. Значит, поле будет отсутствовать внутри полости. Если теперь заземлить данный проводник с полостью, то потенциал во всех точках полости будет равен нулю, т. е. полость полностью является изолированной от влияния внешних электростатических полей. На этом основана электростатическая защита — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Для защиты вместо сплошного проводника может быть использована густая металлическая сетка, которая, также эффективна при наличии не только постоянных, но и переменных электрических полей.

Свойство зарядов располагаться на внешней поверхности проводника на практике используется для устройства электростатических генераторов, которые предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, который изобретен американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 3), укрепленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, которые соединены с одним из полюсов источника, второй полюс которого заземлен. Заземленная пластина 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Значит, сфера постепенно получает большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы широко применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

12. Теорема Остроградского-Гаусса:

Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

Формула

Бесконечная плоскость заряжена с постоянной поверхностной плотностью Формула (Формула — заряд, приходящийся на единицу поверхности).

Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosα = 0),то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания En совпадает с E), т.е. равен 2ES.

Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса Формула , откуда Формула

Из формулы вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

Поле двух бесконечных параллельных разноименно заряженных плоскостей

(рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и −σ. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности.

На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E = 0

В области между плоскостями E+ + E− (E+ и E− определяются по формуле Формула ), поэтому результирующая напряженность: Формула.

Таким образом, результирующая напряженность поля в области между плоскостями описывается этой формулой, а вне объема, ограниченного плоскостями, равна нулю.

13. Вокруг отдельного электрического заряда всегда существует электрическое поле.

Электрическое поле, созданное неподвижным зарядом (или системой неподвижных зарядов), называется электростатическим.

Посредством электростатического поля осуществляется взаимодействие между зарядами. Само понятие поля оказалось весьма плодотворным и широко используется в современной физике. Появление поля означает, что что-то изменилось в окружающем нас пространстве. Математически поле описывается какой-то величиной, меняющейся от точки к точке. Например, можно рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости задан вектор скорости, который может меняться со временем (нестационарное течение), а может и быть постоянным (стационарное течение). Это пример векторного поля. К этому же типу полей относится и поле неподвижных электрических зарядов.

Если в некоторую точку пространства на расстоянии r от заряда q внести другой заряд qпр (назовем его «пробным» зарядом), то на него будет действовать электростатическая сила Кулона со стороны заряда q, обусловленная взаимодействием зарядов q и qпр:

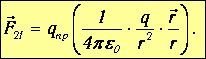
(1.3)

Силы, действующие на один и тот же пробный заряд, в различные точки пространства, будут отличаться и по величине и по направлению (рис. 1.3).

Рис. 1.3. Векторы напряженности электрического поля заряда q в разных точках пространства

Легко видеть, что электрическое поле будет полностью охарактеризовано по величине и по направлению, если найти в каждой точке поля силу, действующую на единичный положительный пробный заряд qпр.

14. Электроемкость — скалярная, физическая величина характеризующая способность проводника или системы проводников накапливать электрический заряд. За величину электроемкости система проводников принимают отношение модуля заряда одного из проводников к разности потенциалов между этим проводником и соседним.

В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Соединение конденсаторов

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Параллельное соединение конденсаторов

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Параллельное соединение конденсаторов формула

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным (рисунок 3).

Последовательное соединение конденсаторов

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заря­жаются через влияние. При этом заряд пла­стины 2 будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряже­ния, существующего на всей группе конденсаторов. Напря­жение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединен­ных последовательно, меньше емкости самого малого конден­сатора в группе.

Для вычисления общей емкости при последовательном со­единении конденсаторов удобнее всего пользоваться следую­щей формулой:

Формула для последовательного соединения конденсаторов

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Формула для последовательного соединения конденсаторов

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Смешанное соединение конденсаторов

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Расчет смешанного соединения конденсаторов

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.

Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники

Конденса́тор (от лат. condense — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

15. Диэлектрик (изолятор) — вещество, практически не проводящее электрический ток. Концентрация свободных носителей заряда в диэлектрике не превышает 108 см−3. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле. С точки зрения зонной теории твёрдого тела диэлектрик — вещество с шириной запрещённой зоны больше 3 эВ.

СВОБОДНЫЕ И СВЯЗАННЫЕ ЗАРЯДЫ

Заряды, которые при приложении внешнего электрического поля могут свободно перемещаться по проводнику, и не связаны с ионами кристаллической решетки, называются свободными.

Заряды, входящие в состав молекулы, которые под действием внешнего поля лишь немного смещаются из своих положений равновесия, и покинуть пределы молекулы не могут, называются связанными.

ПОЛЯРИЗАЦИЕЙ диэлектрика называется процесс ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей.

(Возникновение дипольного момента в диэлектрике называется ПОЛЯРИЗАЦИЕЙ)

В результате поляризации молекула приобретает дипольный момент , величина которого пропорциональна полю

где α – поляризуемость молекулы (характеризует «реакцию» молекулы на электрическое поле). Α – характеристика атома или иона.

В качестве величины, характеризующей степень поляризации диэлектрика, принимается вектор ПОЛЯРИЗОВАННОСТИ - дипольный момент единицы объема (или плотность дипольного момента)

где - дипольный момент одной молекулы , - суммарный дипольный момент объема V.

Трём типам диэлектриков соответствуют три типа поляризации

ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в неполярных молекулах. Электронная поляризация обусловлена смещением электронной оболочки атома относительно ядра во внешнем поле.

ИОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в ионных кристаллах, вызванное смещением подрешеток положительных ионов вдоль поля, а отрицательных – против поля.

ОРИЕНТАЦИОННАЯ (ДИПОЛЬНАЯ) ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в диэлектрике с полярными молекулами вследствие ориентации дипольных моментов молекул по направлению поля.

Между двумя пластинами диэлектриком является воздух. При попытке уменьшить размеры конденсатора, но сохранить его ёмкость, пластины распологают на меньшем расстоянии. Диэлектрических способностей воздуха становится мало. И его заменяют другими более стойкими материалами..

16. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

17/ ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА

Энергия конденсатора приблизительно равна квадрату напряженности эл. поля внутри конденсатора.

Плотность энергии эл. поля конденсатора:

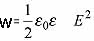
Энергия заряженного конденсатора

Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле (20.1) напряжение между обкладками конденсатора равно

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0.

Среднее значение напряжения в процессе разрядки равно

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:

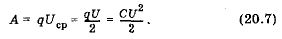
Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна

Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.

18/ СИЛА ТОКА – скалярная физическая велична, равная количеству электрического заряда, переносимосму за единицу времени через поперечное сечение проводника S.

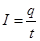
- для постоянного тока, и

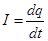
- для переменного тока.

Ток, сила и направление которого не изменяются со временем, называется постоянным.

ПЛОТНОСТЬ ТОКА - векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току.

- для постоянного тока, и

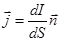
- для переменного тока.

Источник тока - это устройство, в котором происходит преобразование какого-либо вида энергии в электрическую энергию.

В любом источнике тока совершается работа по разделению положительно и отрицательно заряженных частиц, которые накапливаются на полюсах источника.

Существуют различные виды источников тока:

Механический источник тока

Тепловой источник тока

Световой источник тока

Химический источник тока

19/ Падением напряжения (или просто напряжением) на участке цепи 1 – 2 называется величина, численно равная работе электрических и сторонних сил по перемещению положительного единичного заряда на этом участке:

Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называют сторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами)

Сторонние силы, т. е. силы неэлектростатического происхождения. Они действуют лишь внутри источника тока. Разделяя заряды, эти силы создают разность потенциалов между концами остальной части цепи. В этой части движение зарядов обусловлено электрическим полем, возникающим в проводнике вследствие разности потенциалов между его концами.

2 Нравится Ссылка Пожаловаться

20/ 1. Сила тока на участке цепи прямо пропорциональна напряжению на этом участке (при заданном сопротивлении) и обратно пропорциональна сопротивлению участка (при заданном напряжении). I = U / R

2. Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника. I = E / R + r

3. Сила тока (I)- скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шел ток. I = q / t

21. Цель работы: научиться измерять ЭДС источника тока методом компенсации.

Приборы и принадлежности: выпрямитель ПУ-1М, стабилизированный источник питания, два исследуемых гальванических элемента, перекидной шестиполюсный переключатель, гальванометр, реостат, используемый в качестве сопротивления R.

Теоретическая часть

Между полюсами источника тока существует разность потенциалов (напряжение) как в отсутствие тока, когда цепь разомкнута, так и при наличии тока, когда источник замкнут на внешнее сопротивление. Для поддержания этой разности потенциалов внутри источника происходит разделение разноименных зарядов и перенос их на соответствующие полюса источника. Силы, разделяющие заряды, имеют неэлектрическую природу и называются сторонними силами. Природа этих сил может быть разнообразна (химическая, магнитная, механическая и т.д.). Разделению и переносу зарядов внутри источника тока препятствуют, во-первых, внутреннее электрическое поле, во-вторых, сопротивление среды источника. Работа сторонней электроразделительной силы слагается из работы А1, совершаемой против сил электрического поля внутри источника, и работы против механических сил сопротивления среды А2

где

поэтому (1)

Работа, совершаемая сторонней электроразделительной силой при перемещении между полюсами источника тока единичного положительного заряда, называется электродвижущей силой источника.

(2)

Если источник тока разомкнут, то А2 = 0. В этом случае сторонние силы не перемещают заряды внутри источника, а лишь поддерживают установившееся на полюсах разделение зарядов. Поэтому

(3)

т.е. электродвижущая сила равна разности потенциалов на полюсах разомкнутого источника тока. В замкнутой цепи ЭДС равна сумме падений напряжения на внутреннем и внешнем участках цепи

(4)

Методическая часть

Измерение ЭДС исследуемого элемента обычно производят сравнением с ЭДС эталонного источника, которая заранее известна с высокой точностью. Для сравнения ЭДС двух элементов используется компенсационная схема (рис.1).

Вспомогательный источник тока G, замыкается на сопротивление RAB (потенциометр R). Гальванометр Р измеряет силу тока, проходящего через GBX и GC. Включим в цепь сначала эталонный источник GC. Перемещая подвижный контакт потенциометра R, можно добиться равенства нулю тока через GC, (что видно по гальванометру). Отсутствие тока в замкнутом контуре, содержащем ЭДС, возможно только в том случае, если действие ЭДС компенсировано напряжением на некотором участке цепи. В данном случае ЭДС эталонного источника (GC) компенсируется напряжением на участке RAС1, то есть:

(5)

Заменив эталонный источник на исследуемый, также можно добиться компенсации, но при положении подвижного контакта в точке С2. При этом можно записать:

(6)

Так при компенсации разветвления тока в узле Д не происходит (I2=0), то величина тока I определяется только значением ЭДС вспомогательного элемента (?G) и сопротивлением Rab:

и остаётся постоянной при замене GC на GBX- Разделив выражение (5) на (6), получим:

(7)

Поскольку компенсирующее напряжение снимается с потенциометра R, то сравнение электродвижущих сил можно заменить сравнением известных величин сопротивлений в той схеме, в которую включены элементы. В лабораторной установке в качестве внешнего сопротивления R используется потенциометр, выполненный из проволоки с высоким удельным сопротивлением?, намотанной на каркас. Учитывая, что, а проволока имеет одинаковое сечение по всей длине, выражение (7) можно записать в виде:

(8)

где l1 и l2 длины участков RACI и RAC2 соответственно. Потенциометр снабжён равномерной шкалой с делениями, число которых пропорционально длине. В связи с этим формулу (8) можно переписать в виде:

(9)

где NX и NC - число делений на шкале потенциометра при включении GBX и GС соответственно. Зная?Gc и измерив NX и NC, по формуле (9) можно определить ЭДС исследуемого элемента.

Ход выполнения работы

ток электродвижущая сила батарея

Измерения проводим по схеме представленной на рис.2:

Рис.2

Включаем вилку от источника в сеть (~220В). Переключатель S замыкаем на стабилизированный источник питания GC. Передвигаем ручку потенциометра так, чтобы положение стрелки гальванометра было на нуле. По шкале потенциометра определяем число делений NC. Ставим переключатель S в положение GBX.. Передвигая ручку потенциометра R, снова добиваемся отсутствия тока через гальванометр. Определяем число делений потенциометра NX.

Опыт повторяем десять раз и значения заносим в таблицу. Определяем среднее значение NX и NC. Вычисляем ЭДС гальванического элемента по формуле (9), взяв средние значения NX и NC, где - ЭДС исследуемого источника тока, - ЭДС стабилизированного источника питания при комнатной температуре В. Вычисляем погрешность по формуле:

.

Аналогично определяем ЭДС второго элемента.

Результаты измерений

Для первого источника тока:

№ п./п.12345678910Nci144146142146147145146145147147Nxi217216218217218217218219217219

Для второго источника тока:

№ п./п.12345678910Nci147146146145146147147145147146Nxi222221221223221222222223222222

Вычисления

Где f - цена деления линейки.

Для первого источника тока:

В

Для второго источника тока:

В

Вывод

Я научился измерять ЭДС методом компенсаций и получил результаты с небольшими погрешностями для первого источника тока: GBx1=1,52±0,02 В; и для второго: GBx2=1,55±0,02 В. Так как номинал батарей задан 1,5±0,05 В, и вычисленные мною значения входят в этот интервал, следовательно, реальное значение ЭДС этих батарей соответствуют заданному номиналу, и они являются исправными.

22. Закон Ома в дифференциальной форме — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника.

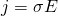
23. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

24. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ

Жидкости по степени электропроводности делятся на:

диэлектрики (дистиллированная вода),

проводники (электролиты),

полупроводники (расплавленный селен).

Электролит

- это проводящая жидкость (растворы кислот, щелочей, солей и расплавленные соли).

25. Биологические ткани и органы являются довольно разнородными образованиями с различными электрическими сопротивлениями, которые могут изменяться при действии электрического тока. Это обусловливает трудности измерения электрического сопротивления живых биологических систем.

Электропроводимость отдельных участков организма, находящихся между электродами, наложенными непосредственно на поверхность тела, существенно зависит от сопротивления кожи и подкожных слоев. Внутри организма ток распространяется в основном по кровеносным и лимфатическим сосудам, мышцам, оболочкам нервных стволов. Сопротивление кожи в свою очередь определяется ее состоянием: толщиной, возрастом, влажностью и т. п.

Электропроводимость тканей и органов зависит от их функционального состояния и, следовательно, может быть использована как диагностический показатель.

Так, например, при воспалении, когда клетки набухают, уменьшается сечение межклеточных соединений и увеличивается электрическое сопротивление; физиологические явления, вызывающие потливость, сопровождаются возрастанием электропроводимости кожи и т. д.

26. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

Сила, действующая на проводник с током, помещенный в магнитное иоле, называется электромагнитной силой. Направление этой силы можно определить по «правилу левой руки»: если левую руку расположить в магнитном поле так, чтобы магнитные линии, выходящие из северного полюса, как бы входили в ладонь, а четыре вытянутых пальца совпадали с направлением тока в проводнике, то большой отогнутый палец руки покажет направление действия силы (рис. 87).

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v заряд q лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического {E} и магнитного {B} полей. В Международной системе единиц (СИ) выражается как:

27. Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией и напряжённостью магнитного поля в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д.).

Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В Международной системе единиц (СИ): 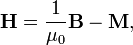где 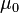— магнитная постоянная.

Магни́тная инду́кция B — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой F магнитное поле действует на заряд q, движущийся со скоростью v.

28. Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма dV проводника с током плотности j, находящегося в магнитном поле с индукцией B, в Международной системе единиц (СИ) имеет вид:

Если ток течёт по тонкому проводнику, то j dV = I d l, где d l — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

29. Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.

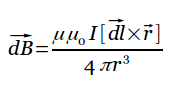
Магнитное поле кругового тока — Создается током текущему по тонкому круглому проводу

30. действие магнитного поля на плоский контур с током определяется магнитным моментом контура 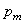, равным произведению силы тока 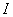в контуре на площадь контура

Магнитный момент является векторной величиной, направленной по нормали к контуру. Из двух возможных направлений нормали выбирается то, которое связано с направлением тока в контуре правилом правого винта (рис. 211). Вращение винта с правой нарезкой в направлении, совпадающем с направлением тока в контуре, вызывает продольное перемещение винта в направлении. Выбранная таким образом нормаль называется положительной. Направление вектора принимается совпадающим с направлением положительной нормали.

31. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

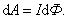
32/ Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Приведем классические опыты Фарадея, с помощью которых было открыто явление электромагнитной индукции.

Опыт I (рис. 1а). Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.

Опыт II. Концы одной из катушек, которая вставлена одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. В моменты включения или выключения тока наблюдается отклонение стрелки гальванометра, а также в моменты его уменьшения или увеличения, а также при перемещении катушек друг относительно друга (рис. 1б). Направления отклонений стрелки гальванометра также имею противоположные направления при включении или выключении тока, его увеличении или уменьшении, приближении или удалении катушек.

опыты Фарадея

Рис.1

Исследуя результаты своих многочисленных опытов, Фарадей пришел к заключению, что индукционный ток возникает всегда, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также появляется индукционный ток - в этом случае индукция магнитного поля вблизи контура остается постоянной, а меняется только поток магнитной индукции сквозь контур.

В результате опыта было также установлено, что значение индукционного тока абсолютно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (также в опытах Фарадея доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения магнита, или скорость изменения силы тока, или скорость движения катушек).

Открытие явления электромагнитной индукции имело огромное значение, поскольку была дана возможность получения электрического тока с помощью магнитного поля. Этим оьткрытие дало взаимосвязь между электрическими и магнитными явлениями, что в дальнейшем послужило толчком для разработки теории электромагнитного поля.

33. Правило Ленца определяет направление индукционного тока и гласит:

Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока \Phi, пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением[1]:

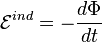
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.

Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменением величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур.

Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.

34. Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур[2][3][4].

В формуле

Ф— магнитный поток, I — ток в контуре, L — индуктивность.

Солено́ид — разновидность электромагнитов. Соленоид — это однослойная катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра. Характеризуется значительным соотношением длины намотки к диаметру оправки, что позволяет создать внутри катушки относительно равномерное магнитное поле.

Соленоид почти всегда снабжается внешним магнитопроводом. Внутренний магнитопровод может быть подвижным или отсутствовать вовсе.

формула для индуктивности соленоида (без сердечника):

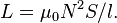
Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников.

35. Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Поиск по сайту: