АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема 1.3. Неопределенный и определенный интегралы и их свойства. Применение определенного интеграла к решению прикладных задач

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  3. I. Решение логических задач средствами алгебры логики
  4. I. Розв’язати задачі
  5. I. Ситуационные задачи и тестовые задания.
  6. II. Основные задачи и функции
  7. II. Решение логических задач табличным способом
  8. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  9. II. Цель и задачи государственной политики в области развития инновационной системы
  10. III. Решение логических задач с помощью рассуждений
  11. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  12. IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.

Практическая работа № 4 «Вычисление неопределенных интегралов»:

Учебная цель: вычислить неопределенные интегралы.

Учебные задачи: научится вычислять неопределенные интегралы.

 

 

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

· Решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления.

знать:

· основные понятия и методы и методы математического анализа;

· алгоритмы применения определенного и неопределенного интеграла;

· основные понятия и методы интегрального исчисления

 

Задачи практической работы:

 

1. Повторить теоретический материал по теме практической работы.

2. Ответить на вопросы для закрепления теоретического материала.

3. Решить вариант.

4. Оформить отчёт

 

Обеспеченность занятия (средства обучения):

1. Тетрадь для практических работ (обычная, в клетку).

2. Карточки-задания (25 штук).

3. Калькулятор (простой).

4. Ручка.

Краткие теоретические и учебно-методические материалы по теме практической работы:

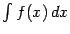Определение Пусть -- функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для называется неопределённым интегралом от и обозначается . Операция нахождения неопределённого интеграла по заданной функции называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функция , записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией.

Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции состоит из функций вида 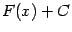, где -- какая-либо фиксированная первообразная для , а -- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция . Поэтому можно написать такую формулу:

(Точнее было бы , но фигурные скобки, обозначающие множество всех функций вида 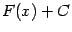, писать в данной ситуации не принято.)

Итак, для того чтобы доказать равенство , достаточно проверить, что -- первообразная для , то есть что .

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)