 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основные законы электрической цепи

Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.

Или

Баланс мощностей используют для проверки правильности расчета электрических цепей.
3. 8 Основные понятия переменного тока. Способы представления синусоидальных величин в векторной и комплексных формах.
Переменный однофазный электрический ток имеет следующие основные характеристики:
f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц (Гц):
1гц = 10 3 кгц = 10 6 мгц
Τ – период – время одного полного изменения переменной величины.
Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц (Герц).
1c = 10 3 мс = 10 6 мкс = 10 12 нс
В Российской Федерации период Τ переменного тока принят равным 0,02 секунды,следовательно по формуле
f = 1/Τ можно определить частоту переменного тока:
f = 1/0,02 = 50 Гц
ω – угловая скорость
Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением:
ω=2πf
При частоте 50 Гц угловая скорость равна 314 рад/с (2 × 3,14 × 50 = 314).
Мгновенное значение (i,u,e,p) – значение величины в данный момент, мгновенное.
Максимальное или амплитудное значение (Im,Um,Em,Pm).
Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t (I,U,E,P).
| I = | Im √2 |
| U = | Um √2 |
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Представление синусоидальных ЭДС, напряжений и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:
показательной  тригонометрической
тригонометрической 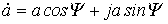 или
алгебраической или
алгебраической  - формах. - формах.
|
Поиск по сайту: