 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Разветвленная электрическая цепь переменного тока. Резонанс токов
Параллельное соединение приемников. Вначале рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.16, а). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей.
Ток в каждой ветви определяется по закону Ома:
| I 1 = | U | ; I 2 = | U | ; I 3 = | U | (xL 3 > xC 3). |
| √ r 12 + xL 12 | √ r 22 + xC 22 | √ r 32 + (xL 3 - xC 3)2 |
Угол сдвига φ между током каждой ветви и напряжением определяют с помощью cos φ:
| cos φ1 = | r 1 | ; cos φ2 = | r 2 | ; cos φ3 = | r 3 | . |
| √ r 12 + xL 12 | √ r 22 + xC 22 | √ r 32 + (xL 3 - xC 3)2 |
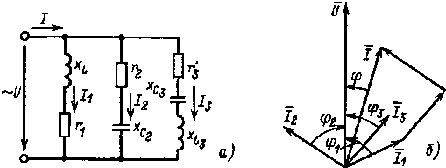
| Рис. 2.16. Цепь с параллельным соединением потребителей (а) и ее векторная диаграмма (б) |
Общий ток в цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов всех ветвей:
Ī = Ī 1 + Ī 2 + Ī 3.
Значение общего тока определяют графически по векторной диаграмме рис. 2.16, б.
Активная мощность цепи равна арифметической сумме активных мощностей всех ветвей:
Р = Р 1 + P 2 + P 3.
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей:
| n | ||
| Q = | ∑ | Qk. |
причем реактивную мощность ветви с индуктивностью берут со знаком плюс, ветви с емкостью — со знаком минус. Для цепи рис. 2.16 реактивная мощность равна
Q = QL 1 - QC 2 + QL 3 - QC 3.
Полная мощность цепи
S = √ P 2 + Q 2.
Угол сдвига φ между общим током и напряжением определяют из векторной диаграммы или из выражения:
cos φ = P/S.
Резонанс токов может возникнуть в параллельной цепи (см. рис. 2.17, а), одна из ветвей которой содержит L и r, а другая С и r.
Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рис. 2.17, г изображена векторная диаграмма цепи рис. 2.17, а при резонансе токов.
Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю:
I 1р = I 2р.
Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю:
I 1р - I 2р = 0.
Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей:
I а = I 1а + I 2а.
Выразив реактивные токи через напряжения и реактивные проводимости, получим
UbL = UbС,
откуда
bL = bС.
Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью.
Выразив bL и bС через сопротивления соответствующей ветви, можно определить резонансную частоту контура:
| xL | = | xC | = | 2π fL | = |
| , | ||
| r 12+ xL 2 | x 22 + xC 2 | r 12 + (2π fL)2 |
|
откуда
| f рез = | √ | L/C - r 12 | . | |
| 2π√ LC | L/C - r 22 |
В идеальном случае, когда r 1 = r 2 = 0,
| f рез = | . | |
| 2π√ LC |
При резонансе токов коэффициент мощности равен единице:
cos φ = 1.
Полная мощность равна активной мощности:
S = P.
Реактивная мощность равна нулю:
Q = QL - QC = 0.
Поиск по сайту: