 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задание 6
|
Читайте также: |
№1. Составить оптимальный план перевозок пищевых продуктов от 4-х поставщиков к 6-ти потребителям. Поставщики (П), потребители (М), объемы вывоза и завоза, кратчайшие расстояния между пунктами вывоза и завоз приведены в таблице.
| Поставщики | Потребители | Объемы вывоза, т | |||||
| М1 | М2 | М3 | М4 | М5 | М6 | ||
| П1 | |||||||
| П2 | |||||||
| П3 | |||||||
| П4 | |||||||
| Объемы завоза, т |
№2. На четыре базы A1, A2, A3, A4 поступил однородный груз в следующем количестве: а1 тонн - на базу А1, а2 тонн - на базу А2, а3 тонн - на базу А3, а4 тонн - на базу А4. Полученный груз требуется перевезти в пять пунктов: b1 тонн - на базу B1, b2 тонн - на базу B2, b3 тонн - на базу B3, b4 тонн - на базу B4, b5 тонн - на базу B5. Расстояния между пунктами назначений указаны в матрице расстояний.
| пункты отправления | пункты назначения | запасы | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| потребности |
Стоимость перевозок пропорциональна количеству груза и расстоянию, на которое этот груз перевозится. Спланировать перевозки так, чтобы их общая стоимость была минимальной.
№ 3. Составить оптимальный план перевозок Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
| Запасы | |||||
| Потребности |
Определение эффективного варианта доставки изделий к потребителю
№4. На складах A1, А2, А3 имеются запасы продукции в количествах 90, 400, 110 т соответственно. Потребители В1, В2, B3 должны получить эту продукцию в количествах 140, 300, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.)

№5. На складах A1, А2, А3 имеются запасы продукции в количествах 95, 85, 110 т соответственно. Потребители В1, В2, B3 должны получить эту продукцию в количествах 140, 30, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.)
№ 6. Найти минимальную стоимость перевозок
| пункты отправления | пункты назначения | запасы | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| потребности |
№ 7. Три нефтеперерабатывающих завода с суточной производительностью 10, 8, 7 млн галлонов бензина снабжают четыре бензохранилища, спрос которых составляет 6, 7, 8 и 5 млн галлонов. Бензин транспортируется в бензохранилища по трубопроводу. Стоимость перекачки бензина на 1 км составляет 5 д.е. на 100 галлонов. Завод 1 не связан с хранилищем 3. Расстояние от заводов до бензохранилищ заданы матрицей  .
.
Распределите план перевозок из условия минимизации транспортных затрат.
№8. На трех железнодорожных станциях А, В, С скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции 1, 2, 3, 4 и 5. На каждой из этих станций потребность в вагонах равна соответственно 80, 60, 70, 100 и 50. Учитывая, что с железнодорожной станции В не предоставляется возможным перегнать вагоны на станции 2 и 4, и зная, что тарифы перегонки одного вагона определяются матрицей  , составьте такой план перегонов вагонов, чтобы общая стоимость была минимальной.
, составьте такой план перегонов вагонов, чтобы общая стоимость была минимальной.
№9. В угольном бассейне добывается уголь, который хранится на трех складах в количестве 120, 60, 100 ед. соответственно. Добытый уголь доставляется четырем энергетическим установкам в количестве 70, 90, 50, и 70 ед. Стоимость доставки 1 ед. угля из каждого склада соответствующим энергетическим установкам задана матрицей  . Определить оптимальный план доставки угля энергетическим установкам, обеспечивающий суммарные минимальные затраты.
. Определить оптимальный план доставки угля энергетическим установкам, обеспечивающий суммарные минимальные затраты.
№10. Три завода выпускают комбайны, которые отправляются потребителям. Первый завод поставляет 50 комбайнов, второй – 40 комбайнов, третий – 70 комбайнов. Каждому из потребителей требуется соответственно 30, 50, 40 и 40 комбайнов. Стоимость перевозки одной единицы техники от поставщика потребителю задана матрицей стоимостей  . Составьте оптимальный план, обеспечивающий общую минимальную стоимость перевозки комбайнов.
. Составьте оптимальный план, обеспечивающий общую минимальную стоимость перевозки комбайнов.
№11. Автомобили перевозятся на трайлерах из трех центров четырем продавцам в количестве 50, 60, 80 и 50 шт. соответственно. В каждом из трех центров находилось соответственно 90, 100 и 50 шт. автомобилей. Стоимость перевозки одной единицы транспортного средства задана матрицей  . Найдите минимальные суммарные затраты на перевозку автомобилей.
. Найдите минимальные суммарные затраты на перевозку автомобилей.
№12. Завод имеет три цеха А, В, С и четыре склада.1, 2, 3, и 4. Цех А производит 30 тыс. шт. изделий, цех В – 40 тыс. шт., цех С – 20 тыс. шт. Пропускная способность складов за то же время характеризуется следующими показателями: склад 1 – 20 тыс. шт., склад 2 – 30 тыс. шт., склад 3 – 30 тыс. шт., склад 4 – 10 тыс. шт. Стоимости перевозки 1 тыс. шт. изделий из цеха А в склады 1, 2, 3, 4 соответственно равны 2, 3, 2, 4 д.е., из цеха В – 3, 2, 5, 1 д.е., из цеха С – 4, 3, 2, 6 д.е. Составить такой план перевозки изделий, при котором расходы на перевозку 90 тыс. шт. изделий были бы минимальными.
№13. На трех автобазах имеются автобусы в количестве 35, 45, 50 шт. соответственно для обслуживания четырех маршрутов. Для перевозки пассажиров каждому из маршрутов требуется автобусов в количестве 40,25, 35 и 30 шт. соответственно. Расходы по эксплуатации каждой транспортной единицы заданы матрицей 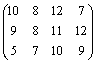 . Распределить имеющиеся транспортные средства (автобусы) по маршрутам таким образом, чтобы общие расходы были минимальными.
. Распределить имеющиеся транспортные средства (автобусы) по маршрутам таким образом, чтобы общие расходы были минимальными.
№14. Три завода выпускают грузовые автомобили, которые отправляются четырем потребителям. Первый завод поставляет 90 платформ грузовиков, второй – 30 платформ, третий – 40 платформ. Требуется поставить платформы следующим потребителям: первому – 70 шт., второму – 30 шт., третьему – 20 шт., четвертому – 40 шт. Стоимость перевозки одной платформы от поставщика до потребителя указана в следующей таблице (д.е.):
| Поставщики | Потребители | |||
| I | II | III | IV | |
| 1 2 3 | 18 10 16 | 20 20 22 | 14 40 10 | 10 30 20 |
Составьте оптимальный план доставки грузовых автомобилей, обеспечивающий минимальные расходы.
№15. На складах А, В, С находится сортовое зерно 100, 150, 250 т., которое нужно доставить в четыре пункта. Пункту 1 необходимо поставить 50 т., пункту 2 – 100 т., пункту 3 – 200 т., пункту 4 – 150 т. сортового зерна. Стоимость доставки 1 т. зерна со склада А в указанные пункты соответственно равна (д. е.) 80, 30, 50, 20; со склада В – 40, 10, 60, 70; со склада С – 10, 90, 40, 30. Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки.
№16. Груз, находящийся на трех складах и требующий для перевозки 60, 80, 106 автомашин соответственно, необходимо перевезти в четыре магазина, Первому магазину требуется 44 машины груза, второму – 70, третьему- 50 и четвертому – 82 машины. Стоимость пробега одной автомашины за 1 км составляет 10 д.е. Расстояния от складов до магазинов указаны в таблице:
| Склады | Машины | |||
| 1 | 2 | 3 | 4 | |
| 1 2 3 | 18 2 12 | 17 7 18 | 6 10 2 | 8 41 22 |
Составьте оптимальный по стоимости план перевозки груза от складов до магазинов.
№17. Имеются два хранилища с однородным продуктом, в которых сосредоточено 200 и 120 т. продукта соответственно. Продукты необходимо перевезти трем потребителям соответственно в количестве 80, 100 и 120 т. Расстояния (в км) от хранилищ до потребителей заданы в таблице:
| Хранилище | Потребители | ||
| 1 | 2 | 3 | |
| 1 2 | 20 60 | 30 20 | 50 40 |
Затраты на перевозку 1 т. продукта на 1 км постоянны и равны 5 д.е. Определите план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.
№18. На трех складах оптовой базы находится товар в количествах, равных соответственно 140, 300 и 180 т. Этот товар необходимо завезти в пять магазинов, каждый из которых должен получить соответственно 90, 120, 230, 180 и 60 т. С первого склада товар не предоставляется возможным перевозить во второй и пятый магазины, а из второго склада в третий магазин было завезено 100 т. товара. Зная стоимости перевозки 1 т. товара с каждого из складов в соответствующие магазины, которые определяются матрицей  , составьте план перевозок, обеспечивающий минимальную общую стоимость перевозок.
, составьте план перевозок, обеспечивающий минимальную общую стоимость перевозок.
№ 19. Строительный песок добывается в трех карьерах и доставляется на четыре строительные площадки. Производительность карьеров за день составляет соответственно 45 т, 35 т, 40 т., Потребности в песке строительных площадок составляют соответственно 30 т, 40 т, 50 т. Транспортные расходы определены матрицей  . Определить план закрепления строительных площадок за карьерами. Обеспечивающий минимальные расходы.
. Определить план закрепления строительных площадок за карьерами. Обеспечивающий минимальные расходы.
№20. Продукция выпускается на трех заводах в количестве 340, 300, 460. Спрос на эту продукцию определяется соответственно в количестве 350, 200, 450 и 100. Транспортные расходы на доставку 1 ед. продукции с i-го завода (i = 1, 2, 3) k-му потребителю (k = 1, 2, 3, 4) определены матрицей 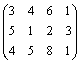 . Определить оптимальный план прикрепления потребителей к заводам из условия минимизации затрат на транспортировку.
. Определить оптимальный план прикрепления потребителей к заводам из условия минимизации затрат на транспортировку.
Поиск по сайту: