АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Олимпиадные задачи для 7 классов. Решить до 26 октября 2014г

Читайте также:
  1. I. Прокурор: понятие, положение, функции и профессиональные задачи.
  2. I. СУЩНОСТЬ, ЦЕЛЬ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
  3. I. ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
  4. II. Задачи территориального фонда
  5. II. ОСНОВНЫЕ ЦЕЛИ И ЗАДАЧИ КОНЦЕПЦИИ
  6. II. Основные цели и задачи Программы, срок и этапы ее реализации, целевые индикаторы и показатели
  7. II. Цели и задачи Конкурса
  8. II. ЦЕЛИ И ЗАДАЧИ КУРСА
  9. III. Задачи Фестиваля
  10. IV. Решите задачи.
  11. IV. Решите задачи.
  12. PR - public relations (общественные связи): цели и задачи, области их использования, инструменты PR.

1.Сколько существует натуральных чисел, каждое из которых превышает сумму своих цифр на произведение этих цифр?

2.В турнире по футболу участвовало 7 команд, которые набрали 14,13,9,8,7,4 и 3 очка. За победу присуждалось 3 очка, за ничью – 1, за поражение – 0 очков. Сколько матчей в турнире закончилось вничью?

3. Найти сумму + + +…+ .

4. Если на каждую палку сядет по 5 галок, то одна галка останется без палки, а если на каждую палку сядет по 6 галок, то одна палка останется пустой. Сколько галок и сколько палок?

5.Грабители угнали 1/3 стада овец и 1/3 овцы. Другая шайка угнала ¼ оставшихся овец и ¼ овцы. Затем третья шайка грабителей угнала 1/5 остатка и ещё 3/5 овцы, после чего в стаде осталось 409 овец. Сколько овец было в стаде первоначально?

6. Найти наименьшее число, делящееся на 7, которое при делении на 2,3,4,5,6 даёт в остатке 1.

7. Имеется 2013 переключателей. Изначально они все включены. Разрешается выбрать любые два и перевернуть их в противоположное положение (выключенные включить, а включённые выключить). Можно ли, проделав несколько раз эту операцию, привести их все во включенное состояние?

8.Существуют ли четыре натуральных числа, сумма и произведение которых нечётны?

9. В классе 27 учеников. Каждый из них написал двум товарищам по записке. Может ли оказаться, что каждый из них получил нечётное число записок?

10. Первая цифра шестизначного числа равна 1. Если её перенести в конец числа, то полученное число будет втрое больше первоначального. Найти первоначальное числою

11. Сколько существует трёхзначных чисел, которые при делении на 7 дают в остатке 2?

12. Сравнить дроб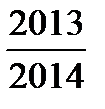и и .

13.Число 7 возвели в 19-ю степень. Полученное число вновь возвели в 19-ю степень и т.д. Возведение повторено 2011 раз. Определить последнюю цифру полученного числа.

14.Три цыплёнка и одна утка проданы за ту же сумму, что и два гуся, а ещё один цыплёнок, две утки и три гуся проданы за 1250 руб. Сколько стоит каждая птица, если цены выражаются целым числом рублей?

15. На сколько сумма всех четных чисел первой тысячи больше суммы всех нечетных чисел той же тысячи?


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)