 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Функция туындысы
Векторлар
1. 
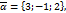
векторлары берілген. Осы векторлардың аралас көбейтіндісін табыңыз.
Шешуі: 
Жауабы: -2
2. 
және 
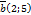векторлары берілген. 
векторының координатасын анықта.
Шешуі: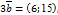 
3. 
және 
векторлары арасындағы бұрыш неге тең?
Шешуі: 
немесе 
болғандықтан 
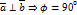
4. 
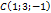төбелері берілген үшбұрыштық ауданын анықтаңыз.
Шешуі: 
, 
, 
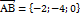5. 
, 
векторлары берілген. Осы векторлардың векторлық көбейтіндісін табыңыз:
Шешуі: 
Жауабы: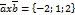 
6. 
векторының ұзындығын табу керек, егер 
, 
болса
Шешуі: 
, 
Жауабы:5.
7. 
және арасындағы бұрыш 
болса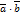 
скалер көбейтіндісін табыңыз:
Шешуі: =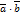 
Жауабы: 5.
8. 
векторларының ұзындығын табу керек, егер 
болса.
Шешуі: 
. Жауабы: 3
9. 
нүктелері берілген 
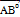бірлік векторының координаталары
Шешуі: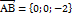 
, 
. 
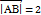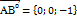
Жазықтықтағы түзу. Шеңбер. Парабола.
1. А(-4;5), В(3;5) нүктелері берілген. Екі нүкте арқылы өтетін түзу теңдеуін жаз.
Шешуі: 
Жауабы: 
2. 
және 
түзулері арасындағы бұрышты тап.
Шешуі: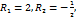 
болғандықтан түзулер перпендикуляр болады. Сондықтан түзулер арасындағы бұрыш 900 –қа тең.
3. 
теңдеуі декраттық координаталар системасында нені анықтайды?
Жауабы: 
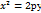- парабола теңдеуі. Олай болса, берілген теңдеуі –парабола теңдеуі.
4. 
нүктесі арқылы ординат осіне параллель өтетін түзу теңдеуін жазыңыз.
Шешуі: 
5. 
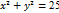теңдеуі декраттық система координатасында нені анықтайды?
Жауабы: Шеңбер.
Функция туындысы.
1. 
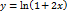функциясының туындысы тең:
Шешуі: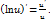 
2. 
функциясының туындысы тең.
Шешуі: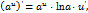 
3. 
функциясының екінші ретті туындысын табыңыз.
Шешуі 
Жауабы: 
4. 
функциясының туындысын табыңыз:
Шешуі: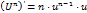 
, 
5. 
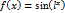функциясының туындысын табыңыз.
Шешуі: 
6. 
функциясының туындысын табыңыз:
Шешуі: 
7. t=1 болғанда 
функциясының неге тең?
Шешуі: 
.
8. 
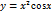функциясының туындысын табыңыз:
Шешуі: 
9. 
функциясының үшінші ретті туындысын табыңыз.
Шешуі: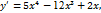 
10. 
функциясының кему аралығын табыңыз.
Шешуі: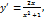 
Кему аралығы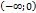 
11. 
функциясының туындысы тең:
Шешуі: 
12. 
кесіндісінде 
функциясының ең үлкен мәнін табыңыз.
Шешуі: 
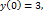
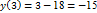
Ең үлкен мәні 3-ке тең.
Көп айнымалылы функция
1. 
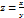функциясының толық дифференциалын табыңыз.
Шешуі: 
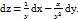
2. 
функциясы берілген. 
мәні неге тең?
Шешуі: 
Дифференциалдық теңдеулер
1. 
дифференциалдық теңдеуінің шешуін табыңыз:
Шешуі: 
Жауабы: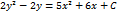 
2. 
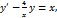
Коши есебін шешіңіз.
Жауабы: 
3. 
екінші ретті дифференциалдық теңдеуді шешіңіз.
Шешуі: 
4. 
дифференциалдық теңдеудің шешуін табыңыз.
Шешуі: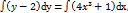 
Жауабы: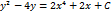 
5. 
теңдеуінің жалпы шешуін анықтаңыз:
Шешуі: 
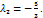
немесе 
Интегралдар
1. 
анықталған интеграл тең:
Шешуі: 
Жауабы: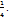 
2. 
3. 
анықталған интеграл тең:
Шешуі: 
Жауабы: 
4. 
интегралын есепте.
Шешуі: Бөліктеп интегралдау формуласын қолданамыз. 
5. 
интегралын табыңыз:
Шешуі: 
6. 
интегралын табыңыз.
Шешуі: 
7. 
үштік интегралын есепте.
Шешу: 
8. 
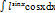интегралын табу үшін мақсатқа сәйкес алмастыруды көрсетіңіз:
Шешуі: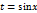 
9. Ньютон – Лейбниц формуласын көрсетіңіз:
Шешуі: 
.
10. Интегралды табыңыз: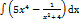 
Шешуі: 
11. 
интегралын табыңыз:
Шешуі: 
12. Анықталған интегралды бөліктеп интегралдау формуласы мынадай:
Жауабы: 
13. 
интегралын есептеңіз, егер 
болса.
Шешуі: 
егер 
.
Сондықтан 
14. 
интегралын есептеңіз.
Шешуі: 
.
15. 
нитегралын есептеңіз.
Шешуі: 
.
16. 
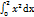анықталған интегралы неге тең?
Шешуі: 
17. 
интегралын табыңыз.
Шешуі: 
18. 
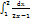анықталған интегралы тең:
Шешуі: 
19. 
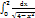анықталған интеграл тең:
Шешуі: 
20. 
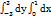интегралын есепте.
Шешуі: 
21. 
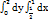қос интегралын есепте.
Шешуі: 
22. Интегралды табыңыз: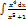 
Шешуі: 
23. 
интегралын есепте.
Шешуі: 
24. 
анықталған интеграл тең:
Шешуі: 
25. 
есептеңіз:
Шешуі: 
Жауабы: 1.
26. 
Шешуі: 
27. Интегралды табыңыз: 
Шешуі: 
28. 
интегралын табыңыз:
Шешуі: 
29. 
түріндегі интеграл рационал бөлшектің интегралына келесі алмастыру көмегімен келтіріледі:
Жауабы: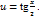 
30. 
анықталмаған интегралын табыңыз:
Шешуі: 
31. 
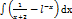интегралын есепте.
Шешуі: 
Қатарлар
1. Дәрежелік қатардың 
жалпы мүшесі келесі өрнек болады
Жауабы: 
Гормониялық қатар дегеніміз не?
Жауабы: 
қатары гормониялық қатар деп аталады, ол жинақсыз қатар.
3. Қатардың жинақты болуының қажетті (қатардың жинақсыздығының жеткілікті шарты)
Жауабы: 
қатары жинақты болса, онда
(
. 
болса қатары жинақсыз)
4. 
жалпы мүшесінің коэфициенті неге тең?
Жауабы: 
5.Сандық қатар дегеніміз не?
Жауабы: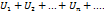 
өрнегі
6. 
қатарының жинақтылық облысын анықта.
Жауабы: (-2;2)
7. 
дәрежелік қатарының жинақтылық радиусын анықтаңыз.
Шешуі: Жинақталу радиусы 
болады.
8. Дәрежелік қатардың 
жалпы мүшесі келесі функция болады:
Жауабы: 
9. 
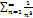(1), 
(2), 
(3), 
(4), 
(5) қатарының қайсысы жинақты, қайсысы жинақсыз?
Жауабы: (1), (3) қатарлары жинақты, (2), (4), (5) қатарлары жинақсыз
10. 
функциясының Маклорен қатарына жіктелуін көрсетіңіз
Жауабы: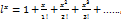 
Эллипс, шеңбер, гипербола, парабола.
1. 
элипісінің эксцентристетін анықтаңыз.
Шешуі: Эллипс теңдеуі: 
, 
-эллипс эксцентристеті 
Жауабы: 
2. 
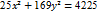теңдеуі қандай қисықты анықтайды?
Шешуі: 
эллипс теңдеуі
3. 
параболасының төбесін анықтаңыз.
Шешуі: 
Жауабы: 
4. 
және 
нүктелері берілген. Диаметрі АВ кесіндісі болатын шеңбердің теңдеуін жаз.
Шешуі: 
шеңбер диаметрі, 
шеңбер радиусы. Шеңбер центрі 
Шеңбер теңдеуі 
теңдеуімен анықталады. 
.
Ізделінді теңдеу 
болады.
Поиск по сайту: