Условные экстремумы

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Частные производные

Пусть - функция двух переменных.

Две частные производные первого порядка:

и (или и ).

Четыре частных производных второго порядка:

, , и (или , , и ).

Если смешанные производные и непрерывны в некоторых точках, то в этих точках выполняется равенство: .

Аналогично определяются производные высших порядков.

Дифференциал первого порядка:

.

Дифференциал второго порядка:

.

Приближенные вычисления с помощью производных

Пусть необходимо вычислить значение функции в точке 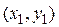, если известно значение функции в точке .

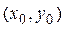Тогда ,

где дифференциал ,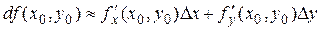

, .

Локальные экстремумы

Алгоритм нахождения локальных экстремумов функции двух переменных :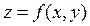

1. Находим первые частные производные и .

2. Решая систему , определяем подозрительные на локальный экстремум точки.

3. Находим вторые частные производные 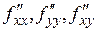и составляем выражение .

4. В каждой подозрительной на локальный экстремум точке вычисляем значения вторых производных и D.

5. Выбираем те точки, для которых D>0. Делаем вывод о наличии в этих точках локального экстремума.

6. Для точек из п.5 определяем вид экстремума: если >0, то в точке локальный минимум, если 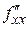<0, то – локальный максимум. Вычисляем значение функции в точках локальных экстремумов.

7. Выбираем из подозрительных на экстремум точек те, для которых D<0. Делаем вывод о том, что в этих точках локального экстремума нет.

Если D в какой-либо точке равно нулю, то вопрос остается открытым.

Условные экстремумы

Алгоритм нахождения условных экстремумов функции 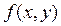при условии, заданном в виде .

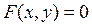1. Составляем функцию Лагранжа .

2. Находим первые производные функции Лагранжа и .

3. Решая систему уравнений , находим подозрительные на условный экстремум точки и соответствующие l.

4. Находим вторые частные производные функции Лагранжа: 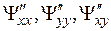и составляем выражение , в котором dx, dy – произвольные переменные приращения.

5. Полученные в п.3 точки и l подставляем в выражение .

6. Находим и . Составляем равенство . Подставляем каждую из подозрительных точек (из п.3) и выражаем через или через .

7. Подставляем найденное выражение из п.6 в выражение из п.5 и приводим к виду или

8. Если >0, то в данной точке условный минимум; если <0, то в данной точке условный максимум. Вычисляем значение функции 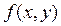в каждой точке условного экстремума.

Поиск по сайту: