 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кінематика гармонічних коливань. Маятники
|
Читайте также: |
Лекція 11. Механічні коливання, їх характеристики та зображення.
План.
1. Поняття про коливальний процес.
2. Кінематика гармонічних коливань. Маятники.
3. Векторні діаграми. Комплексна форма подання коливань.
4. Додавання скалярних та векторних коливань.
1. Поняття про коливальний процес.
Механічне коливання — такий вид руху тіла (матеріальної точки), під час якого воно багаторазово проходить одні й ті ж положення, (при цьому воно багаторазово змінює напрям швидкості). В коливальному русі будь-яка фізична величина набуває однакових значень через рівні, або майже рівні проміжки часу. Крім механічних коливань, в яких повторюються механічні характеристики, в природі поширені електромагнітні коливання, в яких повторюються значення напруги, сили струму, тощо. В пристроях, що перетворюють механічні коливання у електромагнітні та навпаки, відбуваються змішані коливання. Але всі коливальні процеси можуть вивчатися єдиними методами, оскільки мають спільні особливості – періодичне повторення характеристик.
Коливання виникають тоді, коли системі, здатній виконувати коливальні рухи, надається енергія. В консервативних системах ця енергія зберігається, в неконсервативних – зменшується з часом.
Найпростішими є коливання системи жорстко зв’язаних між собою точкових або протяжних об’єктів (маятників). Стан такої системи може бути описаний однією узагальненою координатою (зміщення, кут відхилення, заряд, тиск, тощо). Рух такої системи описується лінійними диференційними рівняннями, що пов’язують узагальнені координати та імпульси системи. Порядок рівнянь визначається кількість ступенів вільності. Так коливання плоского маятника має одну ступінь вільності (зміщення від положення рівноваги) і описується лінійним диференційним рівнянням другого порядку. Подібні системи називають лінійними.
Основна задача теорії коливань полягає у визначенні узагальненої координати  в будь-який момент часу. Коливання називають періодичними, якщо певні значення х повторюються через рівні проміжки часу Т, тобто
в будь-який момент часу. Коливання називають періодичними, якщо певні значення х повторюються через рівні проміжки часу Т, тобто  , де Т - стала величина, яку називають періодом. Якщо умови виконуються не строго, а тільки наближено, коливання називають майже періодичними. Основне в коливальних процесах є зображення коливань у координатах (x;t). Ця залежність характеризує загальний характер коливань.
, де Т - стала величина, яку називають періодом. Якщо умови виконуються не строго, а тільки наближено, коливання називають майже періодичними. Основне в коливальних процесах є зображення коливань у координатах (x;t). Ця залежність характеризує загальний характер коливань.
Особливістю лінійних коливань є незалежність періодичності від наявності чи відсутності дії зовнішніх сил. Для них також справджується принцип суперпозиції: якщо на систему діють незалежні сили, що спричинюють зміну узагальнених координат х1 та х2, то результуюча зміна координат х=х1 +х2.
Хоча реальні коливальні системи завжди нелінійні, їх можна наближено описувати лінійними рівняннями. Таке застосування дає можливість отримувати важливі практичні висновки.
Кінематика гармонічних коливань. Маятники.
Важливими і поширеними є гармонічні коливання, під час яких деякі їх характеристики (наприклад, зміщення тіла з положення рівноваги) змінюються з часом за законом синуса або косинуса. Одержимо рівняння такого коливання:
Коливний процес має багато спільного з рухом по колу. При русі матеріальної точки по колу з положення А у положення В її радіус-вектор обертається на кут  . При цьому проекцію ОЕ радіус-вектора r1 на вісь ОХ позначимо х і назвемо зміщенням матеріальної точки з початкового положення.
. При цьому проекцію ОЕ радіус-вектора r1 на вісь ОХ позначимо х і назвемо зміщенням матеріальної точки з початкового положення.
Можна розглядати проекцію r1 на вісь ОY. У процесі подальшого руху від В до D проекція х зменшується, у — зростає; у другому квадранті кола у зменшується, х зростає і т. д., аж до повернення точки в положення А.
 Отже: при русі матеріальної точки по колу проекції її радіус-вектора здійснюють коливання.
Отже: при русі матеріальної точки по колу проекції її радіус-вектора здійснюють коливання.  , звідки
, звідки 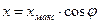
З формули кутової швидкості одержимо  ;
;
Позначимо  , де А – амплітуда.
, де А – амплітуда.
Тоді рівняння гармонічного коливання 
 ,
,
Тоді: 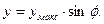 , або:
, або: 

Інші характеристики гармонічного коливання:
1. Аргумент синуса і косинуса називається фазою коливань. Вона визначає, яка частина повного коливання здійснилась на даний момент.
2. Якщо відлік часу почався після початку коливання, кажуть, що коливання відбувається з початковою фазою  , тоді фаза
, тоді фаза  = (
= ( +
+  ).
).
3. Величина  (кутова швидкість обертання) називається циклічною (або круговою) частотою коливання, (кількість коливань за 2π секунди)
(кутова швидкість обертання) називається циклічною (або круговою) частотою коливання, (кількість коливань за 2π секунди)
4. Лінійна частота v- кількість коливань за одиницю часу 
5. Обернена частоті коливання величина — період коливання Т- тривалість одного повного коливання. Зв'язок  , v і Т:
, v і Т:  .
.
Рівняння  є розв’язком диференційного рівняння руху системи, що здійснює гармонічні коливання. Останнє можна отримати, якщо знайти другу похідну за часом:
є розв’язком диференційного рівняння руху системи, що здійснює гармонічні коливання. Останнє можна отримати, якщо знайти другу похідну за часом:
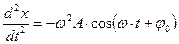 , або
, або 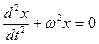
Амплітуду і фазу коливань визначають з початкових умов, що характеризують конкретний процес.
Швидкість та прискорення матеріальної точки знаходіть за допомогою диференціювання за часом:
 , або
, або  ,
,
 , або
, або 
З рівнянь видно, що між коливаннями швидкості та прискорення існує різниця(або зсув) фаз. Коливання швидкості випереджують коливання зміщення на  , а коливання прискорення випереджують коливання зміщення за фазою на π.
, а коливання прискорення випереджують коливання зміщення за фазою на π.
Розглянемо коливання невеличкого тіла на пружині, в якій виникає сила пружності значно більша за силу тяжіння. Опором повітря та масою пружини знехтуємо. Така система називається пружинним маятником. Внаслідок зміщення під положення рівноваги виникає сила пружності, яка визначається за законом Гука:  . Тоді
. Тоді
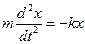 , або
, або 
 , де
, де  . Враховуючи зв’язок циклічної частоти та періоду, знайдемо період коливання пружинного маятника:
. Враховуючи зв’язок циклічної частоти та періоду, знайдемо період коливання пружинного маятника:

Енергія маятника  складається з кінетичної та потенціальної енергій, де кінетична енергія:
складається з кінетичної та потенціальної енергій, де кінетична енергія:  , а потенціальна енергія
, а потенціальна енергія  .
.
Врахуємо, що  та знизимо порядок степеню:
та знизимо порядок степеню:


Отримаємо такі висновки:
1. Циклічна частота коливань енергії вдвічі більша за циклічну частоту коливань зміщення.
2. Повна енергія системи 
3. Середні за період значення кінетичної та потенціальної енергії однакові і дорівнюють 
Математичним маятником називається матеріальна точка, підвішена на довгій, невагомій, нерозтяжній нитці.
Для малих кутів до  його коливання гармонійні, період
його коливання гармонійні, період 
l – довжина нитки;
g – прискорення вільного падіння.
Фізичним маятником називається тіло, здатне коливатися навколо осі коливання, що не співпадє з центром тяжіння.

I – момент енерції тіла відносно осі обертання;
a – відстань від осі обертання до центра тяжіння.
Коливання математичного та фізичного маятників здійснюються за тими ж законами, що й пружинного маятника.
3. Векторні діаграми. Комплексна форма подання коливань.
Розв’язанням лінійного диференційного рівняння другого порядку
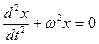
є лінійна комбінація розв’язків: 
Отже, рівняння коливального руху перетворюється у комплексну величину 
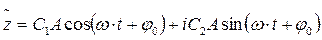
За формулою Ейлера  її можна записати у вигляді:
її можна записати у вигляді:

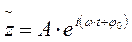
Змінна фізична величина може набувати тільки дійсних значень, тобто

Тоді гармонічні коливання можна зображувати за допомогою векторних діаграм, на яких в полярних координатах зображують вектор  , модуль якого дорівнює амплітуді коливань, а кут між ним та полярною віссю дорівнює початковій фазі. Коливальний рух зображується обертанням цього вектора з кутовою швидкістю ω протии годинникової стрілки.
, модуль якого дорівнює амплітуді коливань, а кут між ним та полярною віссю дорівнює початковій фазі. Коливальний рух зображується обертанням цього вектора з кутовою швидкістю ω протии годинникової стрілки.
Механічну систему, закон руху якої описується рівнянням  , називають одновимірним класичним гармонічним осциллятором або просто класичним осциллятором. Він здійснює коливання навколо положення стійкої рівноваги та описується тими ж рівняннями, що й коливальний рух.
, називають одновимірним класичним гармонічним осциллятором або просто класичним осциллятором. Він здійснює коливання навколо положення стійкої рівноваги та описується тими ж рівняннями, що й коливальний рух.
4. Додавання скалярних та векторних коливань.
У випадках, коли тіло бере участь у кількох коливальних рухах,, результуюче зміщення становитиме геометричну суму незалежних зміщень. Які тіло отримує в кожному русі.
Поиск по сайту: