УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ

Выясним, какими свойствами должна обладать система для того, чтобы в ней могли возникнуть свободные колеба­ния. Удобнее всего рассмотреть вначале колебания шарика, нанизанного на гладкий горизонтальный стержень под действием силы упругости пружины.

Если немного сместить шарик от положения равновесия (рис.1 а) вправо, то длина пружины увеличится на х_п (рис. 1 б), и на шарик начнет действовать сила упругости со стороны пружины. Эта сила согласно закону Гука про­порциональна деформации пружины и направлена влево. Если отпустить шарик, то под действием силы упругости он начнет двигаться с ускорением влево, увеличивая свою ско­рость. Сила упругости при этом будет убывать, так как де­формация пружины уменьшается. В момент, когда шарик достигнет положения равновесия, сила упругости пружины станет равной нулю. Следовательно, согласно второму зако­ну Ньютона станет равным нулю и ускорение шарика.

К этому моменту скорость шарика достигнет макси­мального значения. Не останавливаясь в положении равно­весия, он будет по инерции продолжать двигаться влево. Пружина при этом сжимается. В результате появляется сила упругости, направленная уже вправо и тормозящая движение шарика (рис.1, в).

Вынужденными колебаниями называются колебания тел под действием внешних периодически изменяющихся сил.

Колебания бывают свободными, затухающими и вынуж­денными. Наибольшее значение имеют вынужденные ко­лебания.

Работа внешней силы над системой обеспечивает приток энергии к системе извне. Приток энергии не дает коле­баниям затухнуть, несмотря на действие сил трения.

Особый интерес представляют вынужденные колеба­ния в системе, способной совершить почти свободные коле­бания. С этим случаем знакомы все, кому приходилось раскачивать ребенка на качелях.

Качели — это маятник, т. е. колебательная система с определенной собственной частотой. Отклонить качели на больший угол от положения равновесия с помощью посто­янной во времени небольшой силы невозможно. Не удается раскачать качели и в том случае, если их беспорядочно подталкивать в разные стороны. Однако, если начать в пра­вильном ритме подталкивать качели вперед каждый раз, когда они поравняются с нами, то можно и без большого на­пряжения раскачать их очень сильно. Правда, для этого потребуется некоторое время. Каждый толчок сам по себе мо­жет быть незначительным. После первого толчка качели будут совершать лишь очень малые колебания. Но если темп этих колебаний и внешних толчков один и тот же, то второй толчок будет своевременным и усилит действие пер­вого. Третий усилит колебания еще больше и т. д. Произой­дет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой. Между тем если отдельные толчки следуют друг за другом невпо­пад, то действие одного будет уничтожаться действием сле­дующего, и заметного эффекта не будет.

Вот эта возможность значительного увеличения ампли­туды колебаний системы, способной совершать почти сво­бодные колебания, при совпадении частоты внешней пе­риодической силы с собственной частотой колебательной системы к представляет особый интерес.

Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она дос­тигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика.

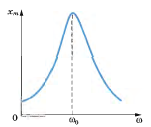При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается. Зависимость ампли­туды колебаний от частоты изображена на рисунке. При очень больших частотах внешней силы амплитуда вы­нужденных колебаний стремится к нулю с ростом частоты, так как тело, вследствие своей инертности, не успевает за­метно смещаться за малые промежутки времени и «дрожит на месте».

Резкое возрастание амплитуды вынужденных колеба­ний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колеба­ний называется резонансом (от латинского слова resonans — дающий отзвук).

Поиск по сайту: