Електромагнітний момент і механічні характеристики трифазного асинхронного двигуна

Обертовий момент будь-якого електродвигуна змінного струму визначається його потоком Ф і активною складовою струму:

М_эм=С_м∙ Ф∙ I₂∙ cosφ₂ (8.6)

где Ф – рабочий поток машины, I₂∙cosφ₂ – активная составляющая тока в фазе ротора, φ₂ – фазовый сдвиг между напряжением и током в фазе ротора, C_м=р∙m₂∙К_об2 – конструктивная постоянная машины, зависящая от числа пар полюсов "р", числа фаз обмоток ротора m₂ (для короткозамкнутого ротора m₂ равно числу стержней обмотки), и обмоточного коэффициента К_об2, который для обмотки типа "беличья клетка" равен 1.

Обертовий момент дозволяє зв'язати величину моменту з фізичними явищами, що відбуваються у двигуні. Однак величини, що входять до формули (Ф, I₂, cosφ₂) не зв'язані явно з напругою мережі живлення і з режимом роботи машини. Тому доцільно вивести формулу, що дозволяє визначити величину електромагнітного моменту через напругу мережі, параметри обмоток і ковзання S машини.

Так як в будь-якій електричній машині у встановленому режимі електромагнітний момент М_эм, що розвивається машиною, дорівнює моменту навантаження на валу машини М, тоді вираз для потужності втрат в міді ротора можна представити у вигляді

Р_м2=М_эм∙ W₁∙ S,

Де W₁=pn₁/30 (рад/с) – кутова швидкість обертання магнітного поля статора.

З відси слідує, що

М_эм=Р_м2/(W₁∙ S).

Оскільки , то використовуючи отриманий раніше вираз для струму у фазі ротора , можемо знайти вираз для електромагнітного моменту машини у вигляді

. (8.7)

Отримана формула показує, що обертаючий момент залежить від квадрата фазної напруги двигуна U₁, від активних і реактивних опорів обмотки ротора R₂, X₂ і від ковзання S.

Залежність моменту М_ЭМ від ковзання при незмінній напрузі і параметрах обмоток від ковзання ілюструється кривою 1 на малюнку 8.16. При малих ковзаннях S момент М_ЭМ зростає з ростом S, досягає максимуму М_ЭМмах при критичному ковзанні S_кр і потім зменшується, досягаючи значення пускового моменту МП при ковзанні S=1. Фізично це пояснюється тим, що у формулі (8.6) при малих ковзаннях переважний вплив має зростання струму у фазі ротора I₂. При S>S_кр струм I₂ зростає мало і переважний вплив чинить зменшення cosφ₂ , де

Кут φ₂ зростає з ростом частоти f₂=f₁∙ S зміни струму у фазі обмотки ротора.

/

Рис.8.16

Отже, критичне ковзання залежить тільки від параметрів фазних обмоток машини R₂, X_2K.

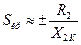(8.8)

З ростом активного опору фази ротора максимум залежності М_ЭМ(S) зміщується в сторони більших ковзань, тобто значення S_кр зростає (крива 2 на малюнку 8.16), при цьому зростає і значення пускового моменту МП двигуна згідно (8.7).

Величина максимального електромагнітного моменту зберігається постійною зі збільшенням 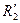, тому що М_ЭМмах не залежить від величини R₂:

(8.8)

Відношення М_ЭМмах/М_ном характеризує перевантажувальну здатність двигуна. (Для двигунів звичайного виконання це відношення становить величину 1,7-2,5).

Відношення М_П/М_ном характеризує пускові властивості двигуна, звичайно ця величина дорівнює 1,2-2,5.

Залежність швидкості обертання ротора n₂ від величини моменту навантаження на валу двигуна при постійній (у змісті діючого значення) фазній напрузі називається механічною характеристикою двигуна. Оскільки швидкість ротора однозначно зв'язана з ковзанням, тобто

n₂=n₁(1-S)

то задаючи значення S і знаючи залежність М_ЭМ(S), можна побудувати механічну характеристику двигуна у вигляді, представленому на малюнку 8.17.

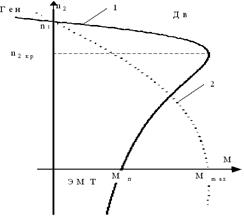
Рис.8.17.

Дослідження механічної характеристики показує, що двигун може працювати стійко лише на ділянці механічної характеристики від n₂=n₁ до n₂=n_2кр=n₁(1-S_кр). Звичайно n_2кр≈(0,8÷0,9) n₁. Під стійкістю тут розуміється здатність двигуна відновлювати сталу частоту обертання при короткочасних змінах навантаження, що живить мережу і т.д. В діапазоні стійкої роботи двигун має властивість саморегулювання, тобто здатність розвивати обертаючий електромагнітний момент, рівний моменту навантаження на валу, тобто М_ЭМ=М.

Умовою стійкої роботи двигуна являється умова

.

Для розширення діапазону стійкої роботи (n₁÷n_2кр) збільшують активний опір фази ротора, так щоб S_кр≥1. Тоді двигун буде працювати стійко в діапазоні швидкостей від 0 до n₁ (крива 2, на мал. 8.17).

Контрольні питання:

1. Чому рівні діючі значення ЕРС обмоток статора і ротора?

2. Як змінюється ЕРС ротора в процесі роботи двигуна?

3. Як визначити струм в обмотціц ротора?

4. Від чого залежить обертовий момент АД?

5. Як можна охарактеризувати перевантажувальну здатність двигуна?

6. Що таке пускові властивості АД?

7. Як будуються механічні характеристики АД?

Поиск по сайту: