Эксперимент 1: моделирование гармонических колебаний. Самостоятельная работа: Численные эксперименты по обработке звука

Самостоятельная работа: Численные эксперименты по обработке звука

График функции Y(x) – наглядное (графическое) отображение зависимости значения функции Y от значения аргумента x. График строится в пределах области определения функции (области изменения аргумента x) и области значений Y. Если у функции бесконечная область определения, то для построения графика выбирается тот ее отрезок, в пределах которого поведение функции наиболее характерно. График периодической функции, как минимум, должен отражать один период изменения значений функции.

Эксперимент 1: моделирование гармонических колебаний

Рассмотрим способ построения графика периодической функции, описывающей гармонические колебания. Гармоническими колебаниями называются периодические изменения со временем некоторой физической величины, описываемые функциями синуса или косинуса. В общем виде они выглядят так:

Y=A·sin(2πνt + φ) или Y=A·cos(2πνt + φ)

Здесь A – амплитуда колебаний; t – время (аргумент функции); ν – частота колебаний, измеряемая в герцах; φ – начальная фаза колебаний.

Период функций sin и cos равен 2π. Значение функции (Y) изменяется в интервале от –А до +А. График функции синус называют синусоидой.

Звуковые колебания, описываемые гармонической функцией, называются гармоническими колебаниями. Чистые музыкальные тона: до, ре, ми и др. представляют собой гармонические звуковые колебания разной частоты. Гармонические звуковые колебания издает камертон – эталонный источник музыкального тона. Гармонические колебания совершает математический маятник. В электрическом колебательном контуре сила тока периодически изменяется по гармоническому закону.

Рассмотрим способ построения графика гармонической функции в среде электронной таблицы. Покажем, как это делается, на примере табличного процессора MS Excel.

Работа происходит в два этапа:

1 – табулирование функции;

2 – построение графика функции.

Полученная электронная таблица представлена на рис.1.12.

Параметрами функции являются частота колебаний ν и амплитуда А. Эти параметры вводятся, соответственно, в ячейки С1 и С2. Значение начальной фазы φ примем равным нулю.

Табулирование – это построение таблицы значений функции на некотором интервале значений аргумента с постоянным шагом. Шаг табулирования (∆t) записан в ячейке G1.

Таблица помещена в ячейки А4:В25. В столбце А расположены значения аргумента – времени t, в столбце В – значения функции Y=A·sin(2πνt). Изменение времени начинается со значения t=0 (ячейка А5). В ячейке А6 записана формула: =A5+$G$1. Далее эта формула копируется в следующие ячейки столбца А. Таким образом обеспечивается изменение времени с постоянным шагом, хранящемся в ячейке G1.

В ячейку В5 заносится формула: =$C$2*SIN(2*ПИ()*$C$1*A5). По этой формуле вычисляется значение функции от аргумента, находящегося в ячейке А5. Стандартная функция ПИ() возвращает значение числа Пифагора π. Формула из ячейки В5 копируется вниз по столбцу до ячейки В25.

На рис.1.12 показаны результаты табулирования функции для значений ν=10 Гц, A=1. Шаг табулирования принят равным 0,005. При частоте 10 Гц период колебаний равен 1/10=0,1 с. При шаге табулирования 0,005 на одном периоде укладывается 20 шагов. Это вполне достаточное количество значений для построения графика функции.

A B C D E F G H I J K L   Частота колебаний:   Гц Шаг табулирования 0,005 c           Амплитуда:                                                 t (с) Y=A·sin(2πνt)                             0,005 0,309016994   0,01 0,587785252   0,015 0,809016994   0,02 0,951056516   0,025     0,03 0,951056516   0,035 0,809016994   0,04 0,587785252   0,045 0,309016994   0,05 5,66604E-16   0,055 -0,309016994   0,06 -0,587785252   0,065 -0,809016994   0,07 -0,951056516   0,075 -1   0,08 -0,951056516   0,085 -0,809016994   0,09 -0,587785252   0,095 -0,309016994   0,1 6,43149E-16

Рис.1.12. Таблица и график гармонической функции

Построение графика. Для графической обработки данных в табличном процессоре существует мастер построения диаграмм и графиков. Его вызов происходит через меню по командам: Вставка – Диаграммы. Дальнейшие шаги алгоритма следующие:

1 –выбрать тип диаграммы: стандартные – точечная, вид – сглаживающие линии

2 – задать диапазон данных (значений функции): в столбцах - В5:В25; закладка РЯД, значения Х: А5:А25

3 – определитьзаголовок: Y=A·sin(2πνt). подписи под осями: t, Y, линии сетки, легенду (нет), подписи данных (нет).

4 – указать, на каком листе книги разметить диаграмму.

ГОТОВО. График построен.

Толщину линий, цвет фона, вид координатной сетки можно настроить отдельно, используя контекстное меню (по правой кнопке мыши), задавая нужные форматы объектов.

Человек слышит звуковые колебания, в среднем, в диапазоне частот от 20Гц до 20кГц. Частота 10 Гц – это частота инфразвука. Некоторые животные воспринимают его на слух. Если же удвоить частоту, то будет достигнута нижняя частотная граница слышимости человека. Но тогда на временном интервале 0,1 секунды поместится два периода колебаний. Такой эксперимент легко выполнить на построенной электронной таблице. Измените значение частоты в ячейке С1 на 20, после чего будет пересчитана таблица, а график примет вид, представленный на рис.1.13.

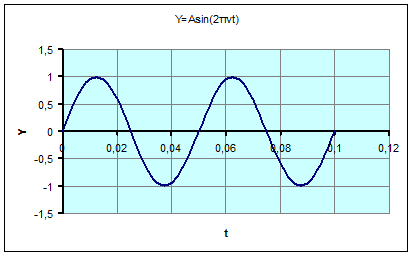
Рис.1.13. График звуковых колебаний для ν=20 Гц

На интервале времени 0,1 секунды уложилось 2 периода функции. Следовательно, период колебаний равен 0,05 секунды.

Задания

1 уровень

Проведите несколько экспериментов с электронной таблицей для значений частоты: 5 Гц, 15 Гц, 30 Гц, 40 Гц. В каждом случае определите, сколько периодов колебаний укладывается в интервал 0,1 секунды?

Поиск по сайту: