АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Статистическая проверка статистических гипотез

Читайте также:
  1. Актуализация опорных знаний. Проверка д/з.
  2. Алгоритм проверки значимости регрессоров во множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки, формулы для расчета статистики.
  3. Американская гипотеза
  4. Взаимная проверка подлинности пользователей.
  5. Вопрос 25. Проверка знаний Правил. Виды проверок. Периодичность проведения проверок.
  6. Вопрос 28. Проверка знаний Правил. Виды проверок. Периодичность проведения проверок.
  7. Вопрос № 21 Специфика статистических материалов как исторического источника. Материалы ревизий как исторический источник.
  8. Выбор аппаратуры защиты отходящих линий и проверка её на срабатывание при однофазном коротком замыкании.
  9. Выездная налоговая проверка (ст 89 НК)
  10. Выездная налоговая проверка, ее назначение и порядок проведения.
  11. Выездная налоговая проверка. Порядок проведения (ст. 89).
  12. ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ СТАТИСТИЧЕСКИХ ПАРАМЕТРОВ

1. Для сравнения точности двух станков-автоматов взяты две пробы X и Y разного объёма. В результате измерения контролируемого размера отобранных изделий получены следующие результаты: X={1,08 1,10 1,12 1,14 1,15 1,25 1,36 1,38 1,40 1,42} и Y={1,11 1,12 1,18 1,22 1,33 1,35 1,36 1,38}. Можно ли считать, что станки обладают одинаковой точностью на уровне значимости 0,1 и конкурирующей гипотезе (т.е. )? Можно ли считать, что станки в среднем выпускают одинаковый контролируемый размер изделий на уровне значимости 0,05 и конкурирующей гипотезе (т.е. )?

2. На уровне значимости 0,05 проверить нулевую гипотезу о равенстве генеральных средних нормальных совокупностей X и Y при конкурирующей гипотезе по малым независимым выборкам:

12,3 12,5 12,8 13,0 13,5
         

 

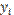
12,2 12,3 13,0
     


3. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х:

0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
                     

Построить гистограммы по экспериментальным и теоретическим частотам на одном графике.

 

4. Используя критерий Пирсона, при уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности Х:

Номер интервала Граница интервала Частота
  -20 -10  
  -10    
       
       
       
       
       

 

5. Для определения засорённости партии семян клевера семенами сорняков было проведено 1000 случайно отобранных проб и получено следующее эмпирическое распределение (в первой строке указано количество
семян сорняков в одной пробе; во второй строке - частота
, т.е. число проб, содержащих семян сорняков):

             
             

 

Требуется при уровне значимости 0,01 проверить гипотезу о том, что случайная величина X (число семян сорняков) распределена по закону Пуассона. Указание: Объединить малочисленные частоты последних двух групп.

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)