ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ СТАТИСТИЧЕСКИХ ПАРАМЕТРОВ

Цель – познакомить студентов с алгоритмом вычисления доверительных интервалов статистических параметров.

При статистической обработке данных вычисленные средние, коэффициенты вариации, коэффициенты корреляции, критерии различия и другие показатели получают количественные границы доверия, которые обозначают возможные колебания показателя в меньшую и большую стороны в пределах доверительного интервала.

Пример 3.1. Распределение кальция в сыворотке крови обезьян, как было установлено ранее, характеризуется следующими выборочными показателями: = 11,94 мг%; 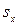= 0,127 мг%; n = 100. Требуется определить доверительный интервал для генеральной средней ()при доверительной вероятности P = 0,95.

Генеральная средняя находится с определенной вероятность в интервале:

, где – средняя арифметическая; t – критерий Стьюдента; 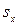– ошибка средней арифметической.

По таблице «Значения критерия Стьюдента» находим значение при доверительной вероятности 0,95 и числе степеней свободы k = 100-1 = 99. Оно равно 1,982. Вместе со значениями среднего арифметического и статистической ошибки подставляем его в формулу:

или 11,69 12,19

Таким образом, с вероятностью 95%, можно утверждать, что генеральная средняя данного нормального распределения находится между 11,69 и 12,19 мг%.

Пример 3.2. Определите границы 95%-ного доверительного интервала для генеральной дисперсии () распределения кальция в крови обезьян, если известно, что 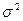= 1,60, при n = 100.

Для решения задачи можно воспользоваться следующей формулой:

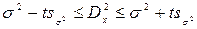, где – статистическая ошибка дисперсии.

Находим ошибку выборочной дисперсии по формуле: 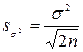. Она равна 0,11. Значение t - критерия при доверительной вероятности 0,95 и числе степеней свободы k = 100–1 = 99 известно из предыдущего примера.

Воспользуемся формулой и получим:

или 1,38 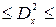1,82

Более точно доверительный интервал генеральной дисперсии можно построить с применением (хи-квадрат)-критерия Пирсона. Критические точки для этого критерия приводятся в специальной таблице. При использовании критерия для построения доверительного интервала применяют двусторонний уровень значимости. Для нижней границы уровень значимости рассчитывается по формуле 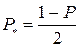, для верхнего – . Например, для доверительного уровня = 0,99 = 0,010, = 0,990. Соответственно по таблице распределения критических значений 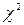, при рассчитанных доверительных уровнях и числе степеней свободы k = 100 – 1= 99, найдем значения и . Получаем равно 135,80, а равно70,06.

Чтобы найти доверительные границы генеральной дисперсии с помощью воспользуемся формулами: для нижней границы , для верхней границы . Подставим данные задачи найденные значения 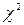в формулы: 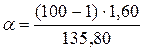= 1,17; = 2,26. Таким образом, при доверительной вероятности P = 0,99 или 99% генеральная дисперсия будет лежать в интервале от 1,17 до 2,26 мг% включительно.

Пример 3.3. Среди 1000 семян пшеницы из поступившей на элеватор партии обнаружено 120 семян зараженных спорыньей. Необходимо определить вероятные границы генеральной доли зараженных семян в данной партии пшеницы.

Доверительные границы для генеральной доли при всех возможных ее значениях целесообразно определять по формуле:

,

Где n – число наблюдений; m – абсолютная численность одной из групп; t – нормированное отклонение.

Выборочная доля зараженных семян равна или 12%. При доверительной вероятности Р = 95% нормированное отклонение (t -критерий Стьюдента при k = ) t = 1,960.

Подставляем имеющиеся данные в формулу:

0,122± 0,041

Отсюда границы доверительного интервала равны 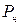= 0,122–0,041 = 0,081, или 8,1%; = 0,122 + 0,041 = 0,163, или 16,3%.

Таким образом, с доверительной вероятностью 95% можно утверждать, что генеральная доля зараженных семян находится между 8,1 и 16,3%.

Пример 3.4. Коэффициент вариации, характеризующий варьирование кальция (мг%) в сыворотке крови обезьян, оказался равным 10,6% или 0,106. Объем выборки n = 100/ Необходимо определить границы 95%-ного доверительного интервала для генерального параметра Cv.

Границы доверительного интервала для генерального коэффициента вариации Cv определяются по следующим формулам:

и , где K промежуточная величина, вычисляемая по формуле .

Зная, что при доверительной вероятности Р = 95% нормированное отклонение (критерий Стьюдента при k = ) t = 1,960, предварительно рассчитаем величину К:

.

или 9,3%

или 12,3%

Таким образом, генеральный коэффициент вариации с доверительной вероятностью 95% лежит в интервале от 9,3 до 12,3%. При повторных выборках коэффициент вариации не превысит 12,3% и не окажется ниже 9,3% в 95 случаях из 100.

Вопросы для самоконтроля:

1. Что такое вероятность?

2. Какие вероятности считаются доверительными?

3. Дайте определение терминов «доверительные границы» и «доверительный интервал».

4. Каков доверительный интервал при нормальном распределении с вероятностью 0,95; 0,99?

5. Что такое уровень значимости? Какая связь между уровнем значимости и вероятностью? Можно ли выражать уровень значимости в процентах?

6. На что указывает процентная величина уровня значимости?

7. В каких пределах по отношению к 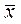выборочной совокупности может находиться средняя арифметическая генеральной совокупности? С какой вероятностью?

8. Изменяются ли доверительные границы и доверительный интервал для μ при разных величинах n? Когда надо пользоваться t – распределением Стьюдента?

Поиск по сайту: