Статистические ошибки точечных оценок

Выборочная средняя, выборочная дисперсия, среднее квадратическое отклонение, коэффициент вариации являются оценками соответствующих генеральных параметров. Это точечные оценки, представляющие собой не интервалы, а числа, вычисляемые по случайной выборке. Выборочные характеристики, как правило, не совпадают по абсолютной величине с соответствующими им генеральными параметрами. Величина отклонения статистики от ее генерального параметра называют статистической ошибкой или ошибкой репрезентативности.

Ошибка средней арифметической вычисляется по формуле

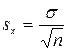, где 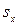– ошибка средней арифметической; σ – среднее квадратическое отклонение; n – объем выборки.

Показатель точности оценки определяется по следующей формуле:

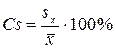
Достоверность средней арифметической оценивается путем сравнения фактического значения критерия Стьюдента с его табличным (или стандартным) значением, которое зависит от числа степеней свободы и принимаемого уровня значимости.

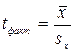, где t – фактический (или наблюдаемый) критерий Стьюдента.

Число степеней свободы для выборочной средней равно k = n – 1.

Обычно используются следующие три уровня значимости в порядке возрастания строгости оценки достоверности биометрических показателей: 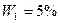, 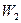=1%, 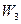= 0,1%. Им соответствуют в том же порядке возрастания строгости оценки, следующие доверительные уровни: 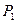= 95%, 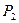= 99%, = 99,9%. И те и другие, также могут быть выражены в долях. Для биологических исследований во многих случаях достаточно принимать 5% уровень значимости, или 95% доверительный уровень, при котором считается достаточным если подтвердится существенность выводов в 95 случаях из 100.

Пример 2.10. Требуется рассчитать статистическую ошибку, показатель точности и достоверность средней арифметической высоты растений сои по данным примера 1. Ранее была рассчитана средняя арифметическая, которая равна 65 см (пример 2.1) и среднее квадратическое отклонение – 12 см (пример 2.7) при n = 13.

Ошибка средней арифметической равна

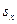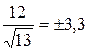= см. (как правило, ошибка записывается с точностью на один знак больше после запятой, чем средняя арифметическая)

Точность определения выборочной средней арифметической равна

Sc = = 5,1%. Она считается вполне удовлетворительной, если коэффициент Sc не превышает 3…5%.

Фактический критерий Стьюдента равен 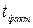= = 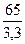19,5, число степеней свободы k = 13–1=12. Табличное значение критерия Стьюдента для 5% уровня значимости равно 2,179 и на 0,15 уровне значимости равно 4,318. Полученное выше значение критерия 19,5 значительно выше табличного, поэтому средняя арифметическая вполне достоверна даже при самой строгой оценке, т.е. на 0,1% уровне значимости.

Пример 2.11. Необходимо сравнить на точность определения средние: = 86,1±0,7 см и 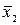= 17,4±0,2 см. Так как средние выражены разными единицами, судить по абсолютной величине их ошибок о том, какая из них определена более точно, нельзя. Ответить на этот вопрос позволяет коэффициент Sc

Sc ; Sc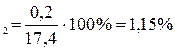

Из расчетов видно, что первая средняя определена более точно, чем вторая.

Пример 2.12. Из 1050 обследованных растений ячменя 66 особей оказалось мутантами, что составляет 6,3% от всего числа растений. Требуется оценить достоверность доли мутантных растений. В задаче имеет место альтернативное распределение. Ошибка доли определяется по формуле:

, где p – доля особей с изучаемым признаком, выраженная часть единицы или в процентах, она же и средняя арифметическая; q – доля особей без этого признака; n – объем всей выборки (1050). Для приведенных данных 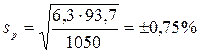. Точность опыта будет равна Sc = 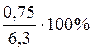= 11,9%, что является низким показателем точности проведенного исследования.

Ошибка среднего квадратического отклонения вычисляется по формуле:

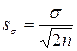или для небольших выборок (при n< 30) по формуле .

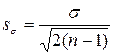Ошибка дисперсии рассчитывается по аналогичной формуле .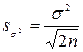

Пример 2.13. Необходимо рассчитать среднее квадратическое отклонение и его ошибку для продолжительности вегетации ячменя, пользуясь данными примера 2.3, где представлен взвешенный вариационный ряд.

Для расчета среднего квадратического отклонения можно воспользоваться формулой 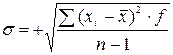где σ – среднее квадратическое отклонение; 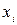– варианты совокупности; f – частота 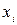; – средняя арифметическая; n – объем выборки. Так как, мы располагаем данными преобразованными во взвешенный вариационный ряд то аналогично с задачей на взвешенную среднюю арифметическую принимаем: 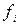– за частоту (математический вес) класса; 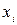– за середину классового интервала. Подставив в формулу данные, получим:

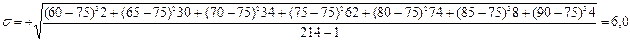
Ошибка среднего квадратического отклонения будет равна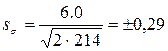

Таким образом, в нашем примере средняя квадратическое отклонение продолжительности вегетации сортов ячменя равно σ = 6 ± 0,3 дня.

Вопросы для самоконтроля:

1. Какие две группы показателей позволяют характеризовать вариационные ряды?

2. Что такое медиана, мода?

3. Что такое размах варьирования и лимиты?

4. Приведите основную формулу средней арифметической.

5. Могут ли совпасть 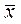, Me, Мо?

6. Свойства средней арифметической.

7. В чем заключается прямой способ вычисления ?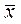

8. Среднее крадратическое отклонение как мерило изменчивости совокупности. Общая формула для него.

9. Степени свободы. Значение этого показателя при вычислении σ и σ². При каких значениях n более точным является использование числа степеней свободы, а не количества вариант (наблюдений)?

10. Формулы для вычисления статистических показателей, если данные не сгруппированы в вариационный ряд.

11. В чем заключается прямой способ вычисления и σ для данных, сгруппированных в вариационный ряд?

12. Какие формулы применяются при непрямом способе вычисления статистических показателей?

13. Можно ли применить условную среднюю для обработки данных, не сгруппированных в вариационный ряд?

14. Почему 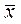и σ являются основными характеристиками вариационного ряда?

15. Какова зависимость между значением ошибки средней и объемом совокупности?

Поиск по сайту: