 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
СОСТАВЛЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Цель – познакомить студентов с принципами группировки первичных данных и основными способами их графического изображения.
Вариационным рядом или рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной статистической совокупности. Вариационный ряд, в котором члены ряда расположены в возрастающем или убывающем порядке называется ранжированным. В зависимости от того, как варьирует признак – дискретно или непрерывно, в широком или узком диапазоне, статистические совокупности могут быть сформированы в безинтервальный или интервальный вариационный ряды. В безинтервальном вариационном ряду частоты относятся непосредственно к ранжированным значениям признака. В интервальном вариационном ряду подсчитывают частоты, относящиеся к отдельным промежуткам или интервалам (классам), на которые разбивается общая вариация признака.
Группировка вариант по классам и составление взвешенных вариационных рядов представляет выборку в легко обозримом виде и облегчает последующие расчеты. Однако любая группировка, при которой истинной значение групп вариант, объединенных в классы, заменяются средними значениями классов, вносит неточность в получаемые затем показатели статистик (хотя и не значительные). В настоящее время, при наличии мощной вычислительно техники, построение вариационных рядов с целью упрощение расчетов потеряло смысл. Вместе с тем, взвешенный вариационный ряд позволяет определить тип и характер распределения признака.
Пример 1.1. На свиноферме зарегистрировано 64 опороса. Количество поросят, полученных от каждой свиноматки, варьировало следующим образом:
8 10 6 10 8 5 11 7 10 6 9 7 8 7 9 11 8 9 10 8 7 8 11 8 7
10 8 8 5 11 8 10 12 7 5 7 9 7 10 5 8 9 7 12 8 9 6 7 8 7
11 8 6 7 9 10
Количество поросят от свиноматки это дискретно варьирующий признак. Объем выборки и ее варьирование относительно не велики. Поэтому совокупность наблюдений следует распределить в безинтервальный вариационный ряд, т.е. непосредственно по ранжированным значениям признака, которые и будут классами данного ряда.
В итоге имеем:
Класс, 
| ||||||||
Частота, 
| ||||||||
Накопленные частоты Σ 
|

Графическим выражением безинтервального ряда будет полигон частот (рисунок).
Для построения кумуляты по оси абсцисс откладывают значения классов, а по оси ординат – накопленные частоты с последующим соединением точек прямыми линиями.

Кумулята распределения количества поросят в помете будет выглядеть следующим образом
Пример 1.2. Имеются данные по продолжительности вегетационного периода (в днях) у 214 сортов ячменя:
66 69 63 77 73 66 72 75 75 80 78 63 75 73 74 80 75 78
68 77 82 75 68 72 84 74 65 73 71 81 80 72 79 75 80 78
84 78 67 84 70 65 79 64 72 77 77 77 82 62 77 69 75 66
69 74 81 91 77 81 78 83 78 80 79 76 77 78 77 77 67 82
80 82 80 82 82 78 79 79 86 72 77 74 76 75 79 79 78 82
80 80 84 80 81 80 76 77 75 76 82 80 78 79 77 68 81 80
75 80 78 79 79 78 80 78 78 76 78 73 65 65 67 76 78 67
71 81 76 78 76 72 75 74 70 70 74 84 76 78 73 70 76 71
74 72 75 81 82 75 73 76 69 72 68 71 80 74 72 80 66 79
78 79 64 68 74 80 64 63 65 64 82 74 64 74 64 64 65 68
60 71 77 68 75 76 67 65 70 66 82 74 80 76 72 78 80 80
69 67 88 92 92 65 73 84 73 71 76 72 78 74 80 80
Требуется построить вариационный ряд и его графическое выражение. Продолжительность вегетационного периода это непрерывно варьирующий признак. Поэтому в этом случае строится не безинтервальный вариационный ряд, а интервальный.
Число классов К можно определить по формуле Стерджеса:  или по таблице
или по таблице
| Число наблюдений, n | Число классов, К |
| 25 – 40 | 5 – 6 |
| 40 – 60 | 6 – 8 |
| 60 – 100 | 7 – 10 |
| 100 – 200 | 8 – 12 |
| > 200 | 10 – 15 |
Обычно при больших выборках число классов принимается от 7 до 15. В данном случае из-за высокого варьирования признака целесообразно игнорировать, расчетное количество классов и принять К = 7.
Рассчитаем величину классового интервала по простой формуле:

Обращаем внимание на то, что точность измерений признака в целых числах, поэтому округляем полученную величину до целого значения. Таким образом, классовый интервал равен  = 5 дням.
= 5 дням.
При построении интервального вариационного ряда желательно поступать так, чтобы минимальная варианта совокупности попадала в середину первого классового интервала. Этому требованию отвечает формула:  , где
, где  – нижняя граница первого класса. Таким образом,
– нижняя граница первого класса. Таким образом,  = 60 – 5/2 = 57,5. Все нижние границы остальных классов получаются путем прибавления к этому значению величины классового интервала, т. е. 5.
= 60 – 5/2 = 57,5. Все нижние границы остальных классов получаются путем прибавления к этому значению величины классового интервала, т. е. 5.
Далее производим разноску вариант (дат) по классам.
Для замены классового интервала на их центральные или средние значения, в результате чего интервальный ряд превращается в безинтервальный ряд, необходимо рассчитать середины классовых интервалов по формуле:  , где
, где  конечная точка интервала. В нашем случае для первого класса
конечная точка интервала. В нашем случае для первого класса 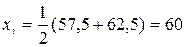 . Середины последующих классов находим путем прибавления к этому значению величины классового интервала.
. Середины последующих классов находим путем прибавления к этому значению величины классового интервала.
В результате получаем:
| Границы класса | Середина класса, 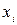
| Частота класса, 
| Частость (относительная частота, %) |
| 57,5 – 62,4 | 0,9 | ||
| 62,5 – 67,4 | 14,0 | ||
| 67,5 – 72,4 | 15,9 | ||
| 72,5 – 77,4 | 29,0 | ||
| 77,5 – 82,4 | 34,6 | ||
| 82,5 – 87,4 | 3,7 | ||
| 87,5 – 92,5 | 1,9 |
Графическим выражением данного вариационного ряда является гистограмма (рисунок).
 |  | ||
Кумулята частот построена по серединам классовых интервалов и выглядит следующим образом:
Пример 1.3. Подсчитано число зерен в початках мутантного образца кукурузы. В 45 початках количество зерен было следующим:
600 671 660 562 495 750 645 500 564 650 640 590 579 450 760 663 516 610 655 637 560 510 710 810 669 496 630 680 641 530 520 720 790 685 535 632 693 674 545 490 715 815 729 825 580
Необходимо построить вариационный ряд и его графическое выражение.
В задаче мы имеем дело с дискретно варьирующим признаком, однако построить безинтервальный ряд в этом случае не возможно. Это связано с высоким уровнем варьирования признака. Поэтому приступим к построению интервального вариационного ряда. По таблице выберем количество классов К = 5.  = 450,
= 450,  = 825. Найдем значение классового интервала, которое равно
= 825. Найдем значение классового интервала, которое равно  = 75. Рассчитаем значение нижней границы первого класса
= 75. Рассчитаем значение нижней границы первого класса  = 450 – 75/2 = 412,5. Округлим это значение до 413, так как имеем дело с дискретно варьирующим признаком. Найдем значения остальных классовых интервалов и распределим по ним даты (варианты). Получим:
= 450 – 75/2 = 412,5. Округлим это значение до 413, так как имеем дело с дискретно варьирующим признаком. Найдем значения остальных классовых интервалов и распределим по ним даты (варианты). Получим:
| Границы класса | Частота класса, 
| Частость (относительная частота, %) |
| 413 – 487 | 2,2 | |
| 488 – 562 | 26,7 | |
| 563 – 637 | 20,0 | |
| 638 – 712 | 31,1 | |
| 713 – 787 | 11,1 | |
| 788 – 862 | 8,9 |
Построим гистограмму числа зерен кукурузы по початкам. Она будет иметь следующий вид:

Вопросы для самоконтроля:
1. Что такое статистическая совокупность?
2. Чем отличается выборочная совокупность от генеральной?
3. Что такое варианта или дата?
4. Какими могут быть отличия между отдельными вариантами?
5. Каковы принципы группировки данных при качественной изменчивости? При количественной дискретной? При количественной непрерывной изменчивости?
6. На сколько классов надо разбивать фактические данные при количественной изменчивости? Целесообразно ли намечать 10 – 15 классов, когда n < 100?
7. Что такое вариационный ряд? Особенности распределения вариант в вариационном ряду?
8. В чем разница между гистограммой и полигоном распределения?
9. Каковы возможные причины многовершинности вариационных кривых?
Поиск по сайту: