Анализ временных рядов и прогнозирование

Задание 18.

Выявите основную тенденцию изменения объема поставок товаров магазину поставщиками за отчетный месяц методом скользящей средней при размерах интервала скольжения р = 3, 5, 7.

Восстановите «потерянные» при сглаживании уровни в начале и конце временного ряда. Представьте результаты в виде таблицы.

Изобразите графически фактический и сглаженные временные ряды в виде линейных диаграмм.

Результаты решения и выводы по ним оформите как приложение 18 к данным методическим указаниям.

Методические указания:

Временной – это ряд числовых значений статистических показателей, расположенных в хронологической последовательности и характеризующих изменение явления во времени.

Временной ряд состоит из двух элементов:

1) уровней ряда– числовых значений статистических показателей, характеризующих величину изучаемого явления– ;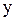

2) периодов (или моментов) времени, к которым относятся данные уровни – .

Одной из основных задач в процессе анализа временного ряда является определение основной закономерности (тенденции) изменений его уровней во времени.

Для выявления и характеристики основной закономерности развития явления проводят выравнивание временных рядов, при котором происходит замена фактических значений уровней ряда расчетными (теоретическими) значениями, имеющими значительно меньшую флюктуацию. При этом систематическая составляющая (тренд) проявляется более ясно, более наглядно.

Различают два вида выравнивания: механическое (или сглаживание) и аналитическое. В среде Excel для механического выравнивания временных рядов используются процедуры Скользящее среднее и Экспоненциальное сглаживание, входящие в Пакет анализа. Приём аналитического выравнивания в Excelреализуется с помощью процедуры Добавить линию тренда, входящей в комплекс графических средств табличного процессора.

При сглаживании временного ряда методом скользящей средней выбирается размер интервала (окна) сглаживания р. Чаще всего его выбирают равным нечетному числу 3, 5 или 7. В этом случае расчетные значения уровней временного ряда можно отнести к фактическому периоду (моменту) времени, для которого имеется фактическое наблюдаемое значение у. Чем больше интервал сглаживания, тем более гладкий вид имеет график скользящего среднего, тем более четко проявляется тенденция. Интервал сглаживания, равный или кратный периоду сезонного колебания, полностью устраняет сезонную компоненту.

При этом «теряются» m = (р-1)/2 уровней в конце и начале исходного временного ряда. То есть он становится короче на р-1 число уровней. Для восстановления «потерянных» уровней в начале и конце сглаживаемого ряда используются следующие формулы:

· для р =3 (m=1):

;

· для р =5 (m=2):

; ;

;

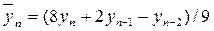Скользящие средние уровни рассчитываются сначала из р первых по порядку уровней временного ряда , затем из р уровней, начиная со второго и так до тех пор, пока не вычислим среднее .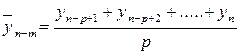

В процессе расчета интервал сглаживания как бы скользит по исследуемому временному ряду с шагом, равным единице (отсюда и название метода). Полученная средняя относится к середине интервала скольжения.

Нахождение средней по четному числу уровней создает неудобство, вызываемое тем, что средняя может быть отнесена только к середине между двумя периодами (моментами). В этом случае нужна дополнительная процедура центрирования средних.

Сглаживание временного ряда методом скользящей средней в Excel осуществляется следующим образом:

1. В диапазон ячеек вводятся уровни временного ряда (числовые значения изучаемого статистического показателя).

2.В меню Сервис выделяется строка Анализ данных.

3. В открывшемся окне Анализ данных выделяется процедура Скользящее среднее и нажимается кнопка ОК. На экране появится диалоговое окно Скользящее среднее.

4. В поле ввода Входной интервал этого окна вводится ссылка на диапазон ячеек, содержащий уровни исследуемого ряда динамики. Входной интервал должен состоять из одного столбца, «высота» которого равна числу уровней данного ряда динамики.

5. В поле Интервал вводится размер окна сглаживания 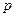(по умолчанию 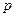=3).

6. В поле Выходной интервал вводится ссылка на верхнюю ячейку столбца результатов сглаживания. Выходной интервал всегда располагается на том же самом рабочем листе, на котором находится входной интервал, поэтому в диалоговом окне процедуры нет таких позиций, как Новый рабочий лист и Новая рабочая книга. Выходной интервал состоит по крайней мере из одного столбца, содержащего уровни сглаженного ряда. Высота этого столбца равна высоте входного интервала. При установке флажка Стандартные погрешности в выходном интервале появляется ещё один столбец– столбец стандартных погрешностей. В точках, для которых нельзя вычислить сглаженные значения и стандартные погрешности, процедура выводит сообщение # Н/Д! (Нет данных).

Для построения линейных диаграмм в меню Вставка выбрать команду Работа с диаграммами → График → Макет.

Задание 19.

Выявите основную тенденцию изменения объема поставок товаров магазину поставщиками за отчетный месяц методом экспоненциального сглаживания с фактором затухания, равным 0,7; 0,8 и 0,9. Представьте результаты в виде таблицы.

Изобразите графически фактический и сглаженные временные ряды в виде линейных диаграмм.

Результаты решения и выводы по ним оформите как приложение 19 к данным методическим указаниям.

Методические указания:

При проведении экспоненциального сглаживания использование одноимённой процедуры аналогично порядку, рассмотренному в задании 14. Вместо поля Интервал диалогового окна Скользящее среднее в процедуре Экспоненциальное сглаживание заполняется поле Фактор затухания. В это поле вводится фактор затухания , где 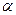– параметр сглаживания (вес текущего значения при вычислении экспоненциального среднего, ). 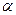Параметр характеризует скорость реакции экспоненциального среднего на изменение текущего значения динамического ряда и одновременно определяет его способность сглаживать случайные колебания. Чем больше 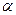, тем быстрее реакция экспоненциального среднего на изменение динамического ряда и тем меньше его сглаживающие возможности. В качестве приемлемого компромисса рекомендуется брать 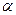в пределах от 0,1 до 0,3. Следовательно, приемлемыми значениями фактора затухания являются значения из интервала от 0,7 до 0,9. В статистической процедуре Экспоненциальное сглаживание по умолчанию 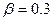, что противоречит рекомендациям.

Метод экспоненциального сглаживания учитывает устаревание данных наблюдения. При его реализации веса уровней временного ряда уменьшаются экспоненциально, в зависимости от «возраста» (давности) наблюдения – текущее наблюдение имеет вес α, а веса предшествующих ему значений равны, соответственно α(1-α), α(1-α)² и т.д. (при использовании метода простого скользящего среднего все усредняемые уровни имеют одинаковый вес, равный 1/ р.

В качестве начального сглаженного значения обычно используют первый уровень исследуемого временного ряда.

Задание 20.

Проведите аналитическое выравнивание месячного объема поставок товаров поставщиками магазину на основе различных аналитических моделей. Выберите модель тренда, имеющую наибольшую аппроксимацию, и охарактеризуйте основную тенденцию.

Постройте точечный и интервальный прогноз объема поставок товаров в первую декаду следующего месяца.

Результаты решения и выводы по ним оформите как приложение 20 к данным методическим указаниям.

Методические указания:

При анализе рядов динамики используются следующие математические модели:

· линейная y_t = a ₀ + a ₁ t,

где и – параметры уравнения;

– начальный уровень тренда в момент или период, принятый за начало отсчёта времени;

– среднее абсолютное изменение за единицу времени;

– обозначение времени.

Параметр определяет направление развития: если , то уровни ряда равномерно возрастают в среднем за единицу времени на величину , если , то происходит их равномерное снижение.

· Полиноминальная (параболическая) , где –степень полинома. Наиболее применяемой в практике статистических расчётов является уравнение параболы второго порядка y_t = a ₀ + a ₁ t + a ₂ t ².

Значение параметров и идентично предыдущему уравнению. Параметр 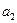характеризует изменение интенсивности развития в единицу времени. При происходит ускорение развития, при – замедление развития.

Соответственно при параболической форме тренда возможны следующие варианты развития:

Ø если ; – ускорение роста;

Ø если ; – замедление роста;

Ø если ; – ускорение снижения;

Ø если ; – замедление снижения.

В уравнении параболы третьего порядка параметр отображает изменение ускорения (замедления):

Ø если ; ; – возрастающее ускорение роста;

Ø если ; ; – замедляющееся ускорение роста;

Ø если ; ; – возрастающее замедление роста;

Ø если ; ; – снижающееся замедление роста;

Ø если ; ; – возрастающее ускорение замедления;

Ø если ; ; – замедляющееся ускорение замедления;

Ø если ; ; – уменьшающееся снижение замедления

Ø если ; ; – возрастающее снижение замедления

· экспоненциальная ,

где – константа ряда, –темп изменения в разах. При >1 экспоненциальный тренд выражает тенденцию ускоренного и всё более ускоряющегося возрастания уровней, при <1 экспоненциальный тренд означает всё более замедляющегося снижения уровней динамического ряда.

· логарифмическая .Логарифмическая форма тренда применяется для отображения тенденции замедляющегося роста уровней при отсутствии предельно возможного значения, например, роста спортивных достижений, производительности агрегата, продуктивности скота.

· гиперболическаяy_t = a ₀ + a ₁ – применяется для отображения тенденции процессов, ограниченных предельным значением уровня;

· степенная – применяется для отображения тенденции явлений с разной мерой пропорциональности изменений во времении др.

Эффективным средством аналитического выравнивания является процедура Добавить линию тренда, входящая в комплекс графических средств табличного процессора Excel. Она вычисляет параметры выбранной пользователем модели тренда. Модель тренда выбирается из набора, включающего в себя пять наиболее распространённых аналитических моделей: линейную, логарифмическую, полиноминальную (параболическую), степенную, экспоненциальную и модель адаптивной скользящей средней (формулы представлены выше). Параметры аналитических моделей вычисляются по данным наблюдения, по которым построен график временного ряда. В результате реализации процедуры в область построения графика выводятся график функции тренда, её аналитическое выражение и значение коэффициента детерминации R².

Для доступа к процедуре Добавить линию тренда необходимо:

1. В диапазон ячеек определённого столбца ввести уровни исследуемого времененного ряда.

2. Построить диаграмму (график) временного ряда.

3. Щелчком на диаграмме активизировать её. На панели меню на месте пункта Данные появится пункт Диаграмма.

4. В пункте меню Диаграмма выбрать команду Добавить линию тренда. Откроется диалоговое окно Линия тренда.

5. В открывшемся окне Линия тренда раскрыть вкладку Тип.

6. На этой вкладке в разделе Построение линии тренда (аппроксимация и сглаживание) выбрать тип (вид) функции тренда.

7. В списке Построен на ряде выделить ряд данных, для которых строится линия тренда.

8. Раскрыть вкладку Параметры диалогового окна Линия тренда.

Эта вкладка содержит следующие элементы управления:

· группу переключателей Название аппроксимирующей (сглаженной) кривой, состоящую из двух переключателей. При установке переключателя автоматическое Excel автоматически присваивает линии тренда имя, связанное с типом этой линии и названием данных наблюдения, по которым строится линия тренда. При установке переключателя другое пользователь сам устанавливает имя линии регрессии и вводит это имя в поле Линейный (Ряд);

· группу счётчиков Прогноз, в которую входят два счётчика: вперёд на…единиц и назад на…единиц. С помощью этих счётчиков устанавливается срок прогноза и производится экстраполяция и интерполяция ряда динамики;

· флажок пересечение кривой с осью Y в точке. Если этот флажок не установлен, ордината точки пересечения линии тренда с осью Y вычисляется по данным наблюдения. Как правило, этот флажок не устанавливается;

· флажок показывать уравнение на диаграмме. При установке этого флажка в область построения диаграммы выводится аналитическое выражение (формула) функции тренда;

· флажок поместить на диаграмму величину достоверности аппроксимации. При установке этого флажка в область построения диаграммы выводится значение коэффициента детерминации R², который показывает, на сколько процентов выбранная линия тренда объясняет разброс уровней ряда. Чем больше данный показатель и чем ближе к единице, тем более точно выбрана линия тренда. Сравнивая величину R² по разным аналитическим моделям можно определить аппроксимирующую функцию, то есть наиболее точно описывающую основную тенденцию развития изучаемого явления.

9. Установить нужные переключатели, счётчики и флажки. Щёлкнуть на кнопке ОК.

В последних версиях Microsoft Office доступ к процедуре осуществляется следующими переходами Вставка → График → Макет → Линии тренда.

Расчет точечного прогноза в случае линейного тренда осуществляется с помощью статистической функции ТЕНДЕНЦИЯ, в случае экспоненциального тренда – с помощью статистической функции РОСТ, при других формах тренда – путем подстановки в построенное уравнение порядковых номеров прогнозируемых периодов (рабочих дней первой декады следующего месяца).

Функции вводятся как функции массива, то есть последовательной комбинацией клавиш Ctrl+Shift+ Enter.

В ячейки какого-либо свободного столбца вводятся порядковые номера прогнозируемых периодов. Выделяется диапазон ячеек, куда будут выведены прогнозные значения (число выделяемых ячеек равно числу прогнозных значений).

Известные значения у – множество значений фактических уровней временного ряда.

Известные значения х – порядковые номера анализируемых периодов: 1,2, 3…. n.

Новые значения х – ссылка на диапазон ячеек, содержащий порядковые номера прогнозируемых периодов.

конст – логическая переменная, определяющая, следует ли включать в уравнение тренда свободный член.

Если конст =1 (ИСТИНА) или опущен, то вычисляются все параметры уравнения тренда, включая свободный член уравнения.

Величина доверительного интервала определяется следующим образом:

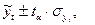где

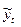- расчетное значение уровня в прогнозируемом периоде (точечный прогноз);

- табличное значение t- критерия Стъюдента при заданном уровне

значимости и числе степеней свободы ;

- средняя квадратическая ошибка уравнения тренда (стандартная ошибка

аппроксимации).

Табличное значение t- критерия Стъюдента определяется с помощью статистической функции СТЬЮДРАСПОБР.

Стандартная ошибка уравнения линейного или полиномиального тренда рассчитывается статистической процедурой Регрессия, в которой данные уравнения могут быть построены, если в качестве входного интервала Х ввести порядковые номера (и их квадраты в случае полиномиального тренда) анализируемых периодов.

Стандартная ошибка уравнения экспоненциального тренда рассчитывается статистической функцией ЛГРФПРИБЛ (см.а «Регрессионный анализ», если в поле ввода Известные значения х ввести порядковые номера анализируемых периодов.

Поиск по сайту: