 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Корреляционный анализ
Задание 11.
С использованием статистической процедуры Пакета анализа Excel Корреляция рассчитайте парный коэффициент корреляции между продолжительностью договорных связей и уровнем выполнения договорных обязательств поставщиков государственной и частой форм собственности. Для этого необходимо предварительно сформировать отдельные выборки поставщиков государственной и частной формы собственности.
Произведите оценку значимости выборочных коэффициентов корреляции у поставщиков и дайте их интерпретацию.
Проверьте значимость статистических расхождений между выборочными коэффициентами корреляции в совокупностях поставщиков государственной и частной форм собственности.
Результаты решения и выводы по ним оформите как приложение 11 к данным методическим указаниям.
Методические указания:
Для количественного измерения степени тесноты связи служат выборочные коэффициенты корреляции. Коэффициент корреляции рассчитывается для определения тесноты и направления связи между двумя коррелирующими признаками. Он может принимать значение от -1 до +1. Отрицательное значение указывает на обратный характер связи между признаками, положительное значение означает, что связь между признаками прямая по направлению. Чем ближе коэффициент корреляции к 1, тем сильнее (теснее) связь между признаками. При словесном описании линейной корреляционной зависимости используются следующие градации:
| Величина коэффициента корреляции | Характер связи |
| до |0,2| | очень слабая |
| |0,2|-|0,4| | слабая |
| |04|-|0,7| | средняя, умеренная |
| |0,7|-|0,9| | сильная |
| |0,9|-|1| | очень сильная |
В Excel вычисление выборочного коэффициента корреляции осуществляется с помощью процедуры Корреляция, входящей в Пакет анализа, и встроенных статистических функций КОРРЕЛ, ПИРСОН и КВПИРСОН.
При применении процедуры Корреляция в поле Входной интервал диалогового окна этой процедуры вводится ссылка на входной диапазон (на диапазон, содержащий данные наблюдения, подлежащие обработке). Входной диапазон должен содержать  смежных столбцов по
смежных столбцов по 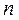 ячеек в каждом столбце или
ячеек в каждом столбце или  смежных строк по
смежных строк по 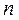 ячеек в каждой строке.
ячеек в каждой строке.
Назначение переключателя Группирование, флажка Метки и группы переключателей Выходной интервал / Новый рабочий лист / Новая книга рассмотрено в первом разделе.
Статистические функции КОРРЕЛ и ПИРСОН вычисляют выборочную оценку линейного коэффициента корреляции, и дублируют друг друга. Синтаксис функции КОРРЕЛ (массив 1; массив 2), где массив 1 – диапазон ячеек, в который введены значения факторного признака (например, А1:А25), а массив 2 – диапазон ячеек, в который введены значения результативного признака (например, В1:В25). Статистическая функция КВПИРСОН вычисляет квадрат выборочного коэффициента корреляции.
Значимость линейного коэффициента корреляции в случае парной корреляции проверяется на основе t – критерия Стьюдента. При этом выдвигается и проверяется гипотеза (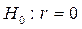 ) о равенстве коэффициента корреляции в генеральной совокупности нулю (то есть в действительности связь между изучаемыми признаками отсутствует, а эмпирическое значение выборочного коэффициента корреляции обусловлено только случайными совпадениями
) о равенстве коэффициента корреляции в генеральной совокупности нулю (то есть в действительности связь между изучаемыми признаками отсутствует, а эмпирическое значение выборочного коэффициента корреляции обусловлено только случайными совпадениями 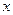 и
и  в выборке). Фактическое (расчетное) значение t – критерия сравнивается с критическим его значением при принятом уровне занятости α и числе степеней свободы k = n-2. В социально-экономических исследованиях уровень значимости α обычно принимается равным 0,05.
в выборке). Фактическое (расчетное) значение t – критерия сравнивается с критическим его значением при принятом уровне занятости α и числе степеней свободы k = n-2. В социально-экономических исследованиях уровень значимости α обычно принимается равным 0,05.
Если расчётное значение t – критерия больше критического, то гипотеза о том, что линейный коэффициент корреляции в генеральной совокупности равен нулю и лишь в силу случайных обстоятельств оказался равен проверяемому значению, отклоняется, то есть коэффициент корреляции признаётся значимым, а связь между признаками – статистически существенной. Если расчётное значение t – критерия меньше критического, то нулевая гипотеза принимается, что означает, что коэффициент корреляции в генеральной совокупности в действительности равен нулю и соответственно эмпирический коэффициент корреляции существенно не отличается от нуля. Фактическое значение t - критерия рассчитывается по формуле - для совокупностей n<50 по формуле:
 ; (*)
; (*)
В Excel проверка гипотезы 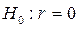 об отсутствии корреляции между изучаемыми признаками осуществляется следующим образом:
об отсутствии корреляции между изучаемыми признаками осуществляется следующим образом:
· В ячейку (например, Н1) вводится значение выборочного коэффициента корреляции 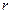 ;
;
· В ячейку Н2 для определения расчётного значения t – критерия вводится формула (*): = Н1*КОРЕНЬ (56/(1-Н1^2)) (если  = 58);
= 58);
· В ячейку Н3 для нахождения критического значения t – критерия Стьюдента при уровне значимости α = 0,05 и числе степеней свободы k =56 вводится формула: = СТЬЮДРАСПОБР (0,025;56);
· Полученные расчётное и критическое значения t – критерия Стьюдента сравниваются, и делается вывод об отклонении или принятии нулевой гипотезы на уровне значимости  =0,025. Если гипотеза
=0,025. Если гипотеза  противоречит реальным данным наблюдения (отклоняется), то выборочный коэффициент корреляции признаётся значимым и между изучаемыми признаками существует соответствующая по степени тесноты корреляционная зависимость. Если гипотеза принимается, коэффициент корреляции признаётся незначимым.
противоречит реальным данным наблюдения (отклоняется), то выборочный коэффициент корреляции признаётся значимым и между изучаемыми признаками существует соответствующая по степени тесноты корреляционная зависимость. Если гипотеза принимается, коэффициент корреляции признаётся незначимым.
Для проверки значимости расхождений между выборочными коэффициентами корреляции двух независимых двумерных выборок объёмов  и
и  выдвигается гипотеза
выдвигается гипотеза 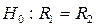 о равенстве коэффициентов корреляции в данных выборках. Альтернативной является гипотеза
о равенстве коэффициентов корреляции в данных выборках. Альтернативной является гипотеза 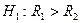 о превышении коэффициентом корреляции в одной выборке коэффициента корреляции в другой выборке. При этом используется критерий, основанный на z -преобразовании Фишера:
о превышении коэффициентом корреляции в одной выборке коэффициента корреляции в другой выборке. При этом используется критерий, основанный на z -преобразовании Фишера:
 ,
,
где 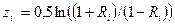 ;
;  – выборочный коэффициент корреляции, найденный по
– выборочный коэффициент корреляции, найденный по 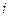 -й выборке (
-й выборке (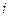 =1,2).
=1,2).
При  принимается гипотеза
принимается гипотеза  , означающая, что расхождение между выборочными коэффициентами незначимо; при
, означающая, что расхождение между выборочными коэффициентами незначимо; при 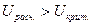 – альтернативная гипотеза
– альтернативная гипотеза 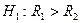 , означающая, что расхождение между выборочными коэффициентами корреляции статистически существенно.
, означающая, что расхождение между выборочными коэффициентами корреляции статистически существенно.
В ячейках F2, F3 и H2, H3 листа «Корреляция» представлен пример расчета (при n1 =43 и n2 =57; R1 = 0,861 и R2 = 0,637). В ячейках F4 и H4 находятся результаты z –преобразования выборочных коэффициентов корреляции, полученные с помощью формул = ФИШЕР (F2) и = ФИШЕР (H2). В ячейке F7 находится расчетное значение U –статистики, вычисленное по формуле = (F4 – H4)/КОРЕНЬ(F6), а в ячейке F8 – критическое значение U –статистики, вычисленное с помощью формулы = НОРМСТОБР (0,95).
Задание 12.
По обобщенным данным за последние пять лет выборочный коэффициент корреляции между продолжительностью договорных связей поставщиков товаров магазину и уровнем выполнения ими договорных обязательств составлял 0,856. Проверьте гипотезу о том, что в отчетном году выборочный коэффициент корреляции между изучаемыми признаками в данной совокупности поставщиков имеет такое же значение.
Результаты решения и выводы по ним оформите как приложение 12 к данным методическим указаниям.
Методические указания:
С помощью статистической процедуры Корреляция вычисляется выборочный коэффициент корреляции по совокупности 100 поставщиков товаров магазину. На основе сравнения расчетного и критического значения t – критерия Стьюдента производится оценка значимости данного коэффициента (порядок расчетов см. в предыдущем задании).
Для проверки гипотезы  о том, что коэффициент корреляции r нормальных случайных величин Х и У равен заданному числу r0 # 0. Используется статистика
о том, что коэффициент корреляции r нормальных случайных величин Х и У равен заданному числу r0 # 0. Используется статистика 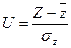 , где
, где 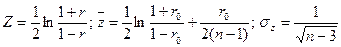 .
.
Если проверяемая гипотеза 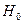 верна, то при п ≥20 статистика U имеет распределение, близкое к стандартному нормальному распределению.
верна, то при п ≥20 статистика U имеет распределение, близкое к стандартному нормальному распределению.
а) При альтернативе 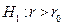 , критическая область размера α имеет вид
, критическая область размера α имеет вид 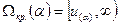 , где
, где  - критическое значение порядка α стандартного нормального распределения.
- критическое значение порядка α стандартного нормального распределения.
б) при альтернативе  критическая область порядка α.
критическая область порядка α. 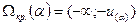
в) при альтернативе 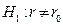
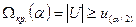
Рассматриваемый критерий основан на z –преобразовании Фишера 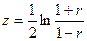 .
.
В Excel имеются функции ФИШЕР и ФИШЕРОБР, реализующие прямое и обратное z –преобразование Фишера.
В ячейку D1 (или в любом другом столбце) записывается значение выборочного коэффициента корреляции r, полученное с помощью процедуры Корреляция.
В ячейку D2 записывается гипотетическое значение коэффициента корреляции r0 =0,856.
В ячейке D3 находят результат Z z –преобразования выборочного коэффициента корреляции r – Z, определяемый с помощью формулы =ФИШЕР(D1).
В ячейке D4 вычисляют значение среднего 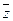 с помощью формулы =ФИШЕР(D2)+ D2/(2∙99).
с помощью формулы =ФИШЕР(D2)+ D2/(2∙99).
В ячейке D5 рассчитывают стандартное отклонение 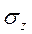 с помощью указанной выше формулы.
с помощью указанной выше формулы.
В ячейке D6 по формуле определяют расчетное значение u статистики U.
В ячейке D7 находят критическое значение 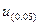 этой статистики по формуле = НОРМСТОБР (0,95).
этой статистики по формуле = НОРМСТОБР (0,95).
На основе сопоставления выборочного коэффициента корреляции r и гипотетического коэффициента корреляции r0 задается альтернативная гипотеза 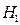 . Определяется критическая область, попадание расчетного значения u-критерия означает, что проверяемая гипотеза
. Определяется критическая область, попадание расчетного значения u-критерия означает, что проверяемая гипотеза 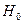 противоречит реальным данным наблюдения и ее надо отклонить и принять альтернативную гипотезу
противоречит реальным данным наблюдения и ее надо отклонить и принять альтернативную гипотезу 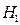 .
.
Поиск по сайту: