Непараметрическая статистика

Задание 15.

С использованием критерия Краскала – Уоллиса по исходным данным задания 9 с вероятностью 95% определите, зависит ли окупаемость затрат в агропромышленных предприятиях от организационно-правовой формы их хозяйствования. Сравните результаты классического и рангового (свободного от распределения) дисперсионного анализа.

Результаты решения и выводы по ним оформите как приложение 15 к данным методическим указаниям.

Методические указания:

Для сравнения нескольких выборок, различных по объёму, применяется критерий Краскала–Уоллиса. Нулевая гипотеза состоит в том, что медианы в совокупностях равны: .

Выборки объединяются, и данные ранжируются в порядке возрастания, как если бы это была единая выборка. Наименьшее значение получает ранг 1, следующее – ранг 2 и т.д. Максимальный ранг равен . Если значения совпадают, им присваиваются связанные ранги, которые определяются как средние из соответствующих порядковых номеров.

По каждой выборке вычисляются квадраты суммы рангов: (),….().

.

Распределение статистики аппроксимируется распределением хи-квадрата при уровне значимости и числе степеней свободы , где – число сравниваемых совокупностей.

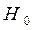Если вычисленное значение статистики превосходит , то нулевая гипотеза отклоняется, что означает наличие статистически существенных различий в уровнях окупаемости затрат в разных ОПФ.

Задание 16.

Измерьте степень тесноты связи между затратами на рекламу магазинов и количеством их клиентов за месяц на основе рангового коэффициента Спирмена. Проведите оценку его значимости. Сделайте выводы.

Результаты решения и выводы по ним оформите как приложение 16 к данным методическим указаниям.

Методические указания:

В случаях, когда анализируется взаимосвязь между количественными признаками, форма распределения которых отличается от нормальной, используются так называемые непараметрические методы. В основу этих методов положен принцип нумерации значений признаков статистического ряда.

Значения факторного признака записываются в возрастающем или убывающем порядке, а затем ранжируются соответствующие им значения результативного признака. При этом каждой единице в упорядоченном ряду присваивается порядковый номер, который будет её рангом. В случаях наличия одинаковых вариантов каждому из них присваивается среднее арифметическое значение их рангов.

Для определения рангов в Excel предусмотрены статистическая процедура Ранг и персентиль и статистическая функция РАНГ.

Использование процедуры Ранг и персентиль заключается в следующем:

1. В меню Сервис выделяется строка Анализ данных.

2. В открывшемся окне Анализ данных выделяется процедура Ранг и персентиль, нажимается кнопка ОК. На экране появляется диалоговое окно Ранг и персентиль.

3. В поле Входной интервал вводится ссылка на диапазон ячеек, содержащий данные, подлежащие ранжированию. Входной диапазон может быть столбцом или группой смежных столбцов (строкой или группой смежных строк). Если входной диапазон представляет собой группу столбцов (строк), то процедура воспринимает каждый столбец (строку) как отдельную выборку.

4. Устанавливается переключатель Группирование в нужное положение (по столбцам или строкам).

5. Флажок Метки устанавливается, если первая строка (столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок не устанавливается.

6. Щелчком на переключателе Выходной интервал активизируется поле ввода, находящее справа от этого переключателя и вводится в него ссылка на левую верхнюю ячейку таблицы результатов решения. В случае необходимости результаты выводятся на Новый рабочий лист или Новую рабочую книгу. Нажимается кнопка ОК.

Процедура определяет порядковый и процентный ранг каждого элемента исследуемой выборки. Ранжировка проводится по выборке, упорядоченной по убыванию, то есть элементу с наибольшим значением признака, присваивается ранг 1.

Результаты решения выводятся на экран в виде таблицы, которая состоит из 4 столбцов: Точка, Столбец (если столбцы с исходными данными имеют свои заголовки, введенные пользователем, Excel использует эти заголовки), Ранг и Процент.

За счет строки заголовков число строк в выходной таблице на единицу больше объема обрабатываемой выборке (это надо учитывать при указании выходного интервала).

В колонку Столбец выводятся элементы выборки, записанные в порядке убывания. Слева от каждого упорядоченного по убыванию элемента колонке Точка указывается номер этого элемента в исходной неупорядоченной выборке.

В столбце Ранг приведены ранги элементов выборки, упорядоченной по убыванию. Чтобы получить эти ранги для неупорядоченной совокупности необходимо результаты решения процедуры отсортировать от минимального к максимальному (Данные- Сортировка).

Если все элементы выборки имеют разные значения признаков, то каждому из них присваивается «персональный» ранг. Если в выборке имеется группа (связка) из k элементов с одинаковыми значениями, то каждому элементу этой связки присваивается один и тот же ранг, равный рангу первого элемента этой связки

В столбце Процент приведены проценторанги элементов выборки. Они показывают процент элементов выборки со значениями изучаемого признака меньше данного значения.

Статистическая функция РАНГ имеет следующий синтаксис: РАНГ (число; массив; порядок):

· число – номер единицы совокупности, ранг которой надо определить. Если необходимо осуществить ранжирование всей совокупности сразу, то вводится диапазон ячеек, в котором находятся данные, подлежащие обработке;

· массив – массив или диапазон ячеек, содержащий единицы исследуемой совокупности (неупорядоченные данные наблюдения);

· порядок – величина, определяющая, как упорядочивать (ранжировать) массив:

– если порядок равен 0 или пропущен, массив упорядочивается в порядке убывания;

– если порядок– любое число, не равное нулю, то массив упорядочивается по возрастанию.

Коэффициент корреляции рангов (Спирмена) определяется по формуле:

r = , где

d – разность между рангами соответствующих величин двух признаков;

n – число единиц в ряду (число пар рангов).

В Excel вычисление коэффициента ранговой корреляции Спирмена осуществляется следующим образом:

1. Вводятся заголовки исходных и расчётных данных, необходимых для расчёта коэффициента корреляции рангов: в ячейку А1– названия единиц изучаемой совокупности, в ячейки В1– название факторного признака, в ячейку С1 – названия результативного признака, в ячейку D3– символ , обозначающий ранг по факторному признаку, в ячейку Е1– символ , обозначающий ранг по результативному признаку, в ячейку– F1– символ , обозначающий квадрат разности между рангами соответствующих величин двух признаков.

2. Производится ввод исходных данных: в диапазон ячеек столбца А вводятся названия или номера единиц изучаемой совокупности; в диапазон ячеек столбца В (В2:В21)– значения факторного признака, в диапазон ячеек столбца С (С2:С21)– значения результативного признака.

3. В диапазонах ячеек D2:D21 и Е2:Е21 определяются соответственно ранги по факторному и результативному признаку с помощью описанной выше процедуры Ранг и персентиль или функции РАНГ, для чего вводятся формулы массива = РАНГ (В2:В21; В1:В21;1) и = РАНГ (С2:С21; С1:С21;1). Функция вводится последовательной комбинацией клавиш Ctrl+Shift+ Enter.

Предварительно диапазон ячеек, в который вводится формула массива необходимо выделить.

Если в формулу массива в поле ввода порядок ввести 0 или оставить его незаполненным, то ранги будут определены по совокупности, упорядоченной по убыванию.

4. В диапазоне F2:F21 вычислить квадраты разности рангов с помощью формулы = (D4-E4)^2 Enter.

5. В ячейках D22, E242 и F22 с помощью кнопки Автосуммирование определить суммы рангов по факторному и результативному признакам и сумму квадрата разности рангов.

6. По формуле рассчитывается выборочная оценка коэффициента ранговой корреляции Спирмена.

Значимость коэффициента корреляции рангов для совокупностей небольшого объёма (n£30) проверяется по таблице предельных значений коэффициента корреляции рангов Спирмена при заданном уровне значимости a и определённом объёме совокупности.

Значимость r может быть проверена также на основе t – критерия Стьюдента. Расчётное значение критерия определяется по формуле:

t_расч⁼ r×

Значение коэффициента корреляции считается статистически существенным, если расчётное значение t – критерия Стьюдента превосходит его критическое значение при заданном уровне значимости a и числе степеней свободы k=n-2. Критическое значение t – критерия определяется с помощью статистической функции СТЬЮДРАСПОБР.

Задание 17.

На торговом предприятии создана экспертная группа из функциональных специалистов с целью выявления сильных и слабых сторон, возможностей и угроз фирмы. Экспертами произведена оценка факторов внешней и внутренней среды (каждый эксперт расположил факторы по их важности и присвоил каждому фактору ранг). Фактор, который имеет, по мнению эксперта, самое важное значение, получает ранг 1, второе по значимости значение – ранг 2 и т. д.) Результаты оценки представлены на листе «Коэффициент согласованности».

Проведите оценку согласованности мнений экспертов на основе коэффициента согласованности (конкордации). Проведите оценку его значимости. Сделайте выводы.

Результаты решения и выводы по ним оформите как приложение 17 к данным методическим указаниям.

Методические указания:

Коэффициент согласованности (конкордации) определяется по формуле:

где – количество факторов; – число экспертов.

Значимость коэффициента конкордации проверяется на основе - критерия Пирсона:

Критическое значение при =0,05 и числе степеней свободы определяется с помощью статистической функции ХИ2ОБР.

Если расчётное значение больше критического значения ( =0,05; ), то можно сделать вывод, что с вероятностью 95% значение коэффициента конкордации статистически значимо.

Поиск по сайту: