Регрессионный анализ

Задание 13.

С использованием статистической процедуры Пакета анализа Excel Регрессия проведите парный регрессионный анализ зависимости уровня выполнения договорных обязательств от продолжительности договорных связей поставщиков с магазином при линейной и нелинейной (полиномиальной и показательной (экспоненциальной)) форме связи.

Постройте уравнения линейной, полиномиальной и экспоненциальной регрессии. Осуществите оценку их адекватности.

Укажите форму связи, которая обеспечивает наилучшую аппроксимацию. Для этого рассчитайте относительные ошибки аппроксимации построенных уравнений регрессии.

Произведите прогнозирование уровня выполнения договорных обязательств при продолжительности договорных связей с магазином 17 лет. Сделайте выводы.

Результаты решения и выводы по ним оформите как приложение 13 к данным методическим указаниям.

Методические указания:

Регрессионным анализомназываются методы исследования формы корреляционной зависимости между изучаемыми признаками единиц исследуемой совокупности. В регрессионном анализе различают парную и множественную регрессию. Парная регрессия описывает связь между двумя признаками: факторным и результативным. Множественная регрессия описывает зависимость результативного признака от нескольких факторных признаков.

Регрессионный анализ включает в себя следующие основные этапы:

· выбор модели регрессии;

· оценка параметров выбранной модели регрессии;

· проверка значимости параметров модели регрессии и их интерпретация;

· проверка адекватности построенной модели регрессии.

При анализе линейной связи применяется прямолинейная функция, математическим выражением которой является уравнение прямой линии: y_x=b₀ +bx. При анализе полиномиальной связи используется уравнение параболы 2-ого порядка: y_x= b₀+b1x+ b2x². При анализе экспоненциальной связи уравнение регрессии может быть записано в следующем виде: y_x= b₀b^x, а также y_x=ехр (b₀ '+b'х), где а' = ln; b' = lnb.

Решение математических уравнений связи предполагает вычисление по исходным данным их параметров a, b1 и b2. Параметры b₁,… b_n в уравнении регрессии называют коэффициентами регрессии.

В Excel для проведения регрессионного анализа существует статистическая процедура Регрессия, позволяющая осуществлять парную линейную, параболическую (полиноминальную) и множественную регрессии.

Парная линейная регрессия в Excel осуществляется следующим образом:

1. Осуществляется ввод исходных данных, т.е. значений факторного (X) и результативного (Y) признака.

2. В окне Анализ данных выделяется процедура Регрессия и нажимается кнопка ОК. Откроется диалоговое окно Регрессия с пульсирующим курсором в поле ввода Входной интервал Y.

3. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения результативного признака Y. В поле ввода Входной интервал Y появится соответствующая ссылка.

4. Осуществляется переход в поле ввода Входной интервал Х. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения факторного признака Х. В поле ввода Входной интервал Х появится соответствующая ссылка.

5. Устанавливается флажок в группе флажков Остатки. В данную группу входят следующие флажки:

– флажок Остатки. При его установке на экран выводится таблица ВЫВОД ОСТАТКОВ, в состав которой входит столбец Остатки;

– флажок График остатков. При активизации этого флажка на экран выводятся графики зависимости остатков от регрессионных переменных (по одному графику на каждую переменную);

– флажок Стандартизированные остатки. При установке данного флажка в таблицу ВЫВОД ОСТАТКОВ добавляется столбец центрированных нормированных (стандартизированных), которые получаются из остатков 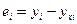делением их на ;

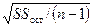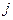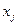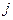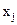– флажок График подбора. При установке этого флажка на рабочий лист выводятся точечных графиков (по числу контролируемых переменных). На графике, связанном с -й контролируемой переменной , =1, 2…., , каждому значению этой переменной поставлены в соответствие две точк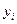и и ;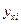

– флажок График нормальной вероятности. При активизации этого флажка на экран выводятся таблица ВЫВОД ВЕРОЯТНОСТИ и график функции, обратной эмпирической функции распределения результативного признака, выполненный на «вероятностной нормальной бумаге».

6. Щелчком на кнопке ОК запускается процедура Регрессия.

Помимо этого процедура содержит также следующие элементы управления:

· Флажок Константа-ноль. Устанавливается в том случае, когда необходимо, чтобы линия регрессии проходила через начало координат. При этом параметр равен нулю и число параметров регрессии равно числу факторов.

· флажок Уровень надёжности. Устанавливается в том случае, когда помимо доверительных интервалов для параметров регрессии, соответствующих используемой по умолчанию «стандартной» доверительной вероятности 95%, необходимо вычислить доверительные интервалы, доверительная вероятность которых отличается от «стандартной». «Нестандартная» вероятность, выраженная в процентах, вводится в поле, расположенное справа от рассматриваемого флажка. Если этот флажок не установлен, то выходной таблице параметров регрессии будут одинаковые пары столбцов, содержащие доверительные границы для параметров регрессии, соответствующие одной и той же доверительной вероятности 95% (при редактировании таблицы их можно убрать).

После запуска процедуры Регрессия на рабочем листе появляются три таблицы результатов этой процедуры. В первой таблице «Регрессионная статистика» содержатся значения множественного коэффициента корреляции, коэффициента детерминации, нормированного коэффициента детерминации, стандартная ошибка уравнения регрессии и число наблюдений.

Множественный коэффициент корреляции 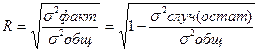; в случае парной линейной регрессии этот показатель совпадает с коэффициентом корреляции 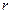, а в случае парной нелинейной регрессии носит название теоретического корреляционного отношения;

Коэффициент детерминации – 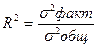; показывает вариацию результативного признака, обусловленную вариацией факторов, входящих в регрессионную модель;

Нормированный (скорректированный) коэффициент детерминации – 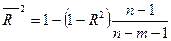. где –число факторов, включённых в регрессионную модель. Корректировка не производится при условии, если ;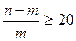

Стандартная ошибка аппроксимации (средняя квадратическая ошибка) уравнения регрессии:

;

где 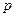-число параметров в уравнении регрессии.

Во второй таблице «Дисперсионный анализ» содержатся значения следующих выборочных характеристик: суммы квадратов (SS) и средний квадрат (MS) отклонений теоретических (расчётных, выровненных) значений результативного признака 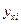от его среднего значения 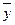; суммы квадратов и среднего квадрата отклонений фактических значений результативного признака 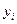от его теоретических значений 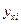; суммы квадратов и среднего квадрата отклонений фактических (эмпирических) значений результативного признака 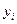от его среднего значения 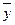; а также расчётное значение критерия Фишера–Снедекора.

Общая сумма квадратов 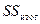= 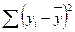– сумма квадратов отклонений фактических (эмпирических) значений результативного признака 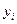от его среднего значения ;

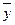сумма квадратов, обусловленная регрессией 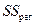= –сумма квадратов отклонений теоретических (расчётных, выровненных) значений результативного признака 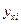от его среднего значения ;

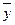сумма квадратов остатков 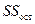= 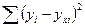–сумма квадратов отклонений фактических значений результативного признака 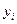от его теоретических значений ;

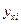числа степеней свободы этих сумм .

средний квадрат регрессии или факторная (систематическая) дисперсия – 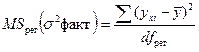– характеризует колеблемость результативного признака под влиянием только фактора х, входящего в уравнение регрессии;

средний квадрат остатков или остаточная (случайная) дисперсия – 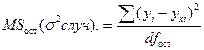–характеризует колеблемость результативного признака под влиянием прочих факторов, не входящих в уравнение регрессия.

Эти дисперсии связаны между собой равенством, носящим название «правило сложения дисперсий»– ; .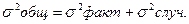

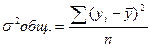Расчётное значение критерия Фишера–Снедекора, вычисляется по формуле: ,

В третьей таблице в графе «Коэффициенты» по строке «Y- пересечение» находится значение свободного члена уравнения регрессии , а по строке Х – значение параметра 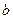. Далее по графам расположены стандартная ошибка параметра регрессии, расчётное значение t – критерия Стьюдента, доверительные интервалы для этих параметров.

Адекватность уравнения регрессии проверяется в два этапа.

1) Проверяется значимость коэффициента детерминации: выдвигается гипотеза 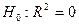о том, что коэффициент детерминации генеральной совокупности, из которой извлечена исследуемая выборка, равен нулю. Эта гипотеза равносильна гипотезе о том, что ни один из факторов, включённых в регрессию, не оказывает существенного влияния на результативный признак (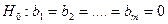). Поэтому проверка значимости коэффициента детерминации является проверкой адекватности (соответствия) выбранной модели регрессии реальным данным наблюдения. В качестве альтернативы рассматривается гипотеза 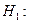хотя бы один коэффициент регрессии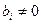

Оценка значимости коэффициента детерминации осуществляется с помощью F-критерия (см. таблицу «Дисперсионный анализ»). Если 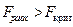, то гипотеза о равенстве коэффициента детерминации нулю и несоответствии заложенных в модели связей реально существующим отклоняется на уровне значимости 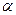, то есть коэффициент детерминации признаётся статистически значимым, а модель регрессии – адекватной. Отклонение проверяемой гипотеза 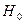в пользу альтернативы 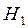означает, что, по крайней мере, один из m факторов, включенных в регрессию оказывает существенное (значимое) влияние на результативный признак.

Величина 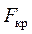определяется с помощью статистической процедуры FРАСПОБР при вероятности 0,05 и числе степеней свободы 1 = df (регрессия) и степеней свободы 2 - df (остаток).

Оценка адекватности коэффициента детерминации может быть произведена на основе преобразованной значимости α*= Значимость F. Если α*<α=0,05 (заданного уровня значимости), это означает, что коэффициент детерминации, надежен, и наоборот.

2) Если гипотеза 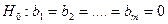отклоняется в пользу альтернативы 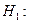хотя бы один коэффициент регрессии 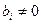, то переходят ко второму этапу – выясняют, какой из коэффициентов регрессии привёл к отклонению гипотезы 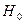. На этом этапе последовательно одна за другой последовательно одна за другой проверяются гипотезы 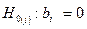о том, что фактор 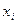не оказывает заметного влияния на результативный признак. В качестве альтернативы рассматривается гипотеза .

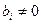То есть на данном этапе производится оценка значимости параметров уравнения регрессии.

Значимость параметров регрессии проверяется на основе t – критерия Стьюдента.

Параметр признаётся статистически значимым, если расчётное значение t – критерия Стьюдента (t –статистика) превосходит его критическое значение, определяемое при заданном уровне значимости α =0,05 и числе степеней свободы 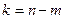. Критическое значение t – критерия может быть определено по таблице распределения Стьюдента или в Excel с помощью статистической функции СТЬЮДРАСПОБР.

Оценка адекватности производится также по значимости α*= Р - значение. Если α*<α=0,05, это означает, что коэффициент регрессии адекватен, надежен. Если α*> α=0, 05, это означает, что коэффициент регрессии несущественно отличатся от нуля.

Оценка значимости параметров уравнения регрессии можно осуществить на основе доверительного интервала коэффициентов регрессии, нижняя и верхняя граница которого определяется соответственно по графе «Нижние 95%» и «Верхние 95%». Если данный интервал не содержит нулевого значения коэффициента регрессии, то коэффициент признается значимым, и наоборот.

При анализе адекватности уравнения регрессии фактическим данным наблюдения возможны следующие варианты:

· построенное уравнение на основе её проверки по F- критерию Фишера в целом адекватно, и все коэффициенты регрессии значимы. Такое уравнение может быть использовано для принятия решений и осуществления прогнозов;

· уравнение по F- критерию Фишера адекватно, но часть коэффициентов регрессии незначима. В этом случае уравнение пригодно для принятия некоторых решений, но не для производства прогнозов;

· уравнение по F- критерию Фишера адекватно, но все коэффициенты регрессии незначимы. В этом случае уравнение полностью считается неадекватным. На его основе не принимаются решения и не осуществляются прогнозы;

· уравнение по F- критерию Фишера неадекватно, и все коэффициенты регрессии незначимы. В этом случае уравнение полностью считается неадекватным. На его основе не принимаются решения и не осуществляются прогнозы.

Полиноминальная (параболическая) регрессия в Excel осуществляется следующим образом:

1. В ячейки А1, В1 и С1 вводятся метки Y, X и X².

2. В диапазон А2 и далее (например, А2: А101) вводятся значения результативного признака Y, в диапазон В2 и далее (соответственно В2:В101)– значения факторного признака X.

3.В диапазон С2 и далее (С2: С101) вводится формула массива = В2:В101^2 и нажимается комбинация клавиш Ctrl+Shift+ Enter. В диапазоне С2:С101 появится столбец квадратов значений факторного признака X².

4. В открывшемся окне Анализ данных выделяется процедура Регрессия и нажимается кнопка ОК. Откроется диалоговое окно Регрессия с пульсирующим курсором в поле ввода Входной интервал Y.

5. Осуществляется переход в поле ввода Входной интервал Х. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения факторного признака Х и их квадрат X² (В1:С15). В поле ввода Входной интервал Х появится соответствующая ссылка.

После запуска процедуры Регрессия на рабочем листе появляются три таблицы результатов этой процедуры.

Построение и оценка адекватности уравнения регрессии производится аналогичным образом.

Построение уравнения показательной регрессии осуществляется с помощью статистической функции ЛГРФПРИБЛ.

Функция ЛГРФПРИБЛ вычисляет выборочные оценки параметров показательной (экспоненциальной) регрессии. Синтаксис данной функции: ЛГРФПРИБЛ (известные значения у; известные значения х;, конст; стат):

· известные значения у – множество значений результативного признака. Данный массив представляет собой вектор-столбец размером ;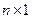

· известные значения х –множество значений факторных признаков.

– Если в случае парной регрессии этот аргумент опущен, то при вычислениях в качестве массива известные значения х используется массив натуральных чисел 1,2…и т.д. такого же размера, как и массив известные значения у;

– В случае множественной регрессии, если массив известные значения у представляет собой вектор-столбец, то массив известные значения х должен иметь строк и столбцов. При этом каждый столбец этого массива содержит значений определённого факторного признака;

– При вводе массива чисел известные значения х с клавиатуры для разделения значений в одной строке используют точку с запятой, а для разделения строк– двоеточие.

· конст –логическая переменная, определяющая, следует ли включать в уравнение регрессии свободный член.

– Если конст =1 (ИСТИНА) или опущен, то вычисляются и коэффициенты регрессии, и свободный член.

– Если конст = 0 (ЛОЖЬ), то предполагается, что свободный член равен единице.

· стат – логическая переменная, определяющая объём выходной информации.

– Если аргумент стат =0 (ЛОЖЬ) или опущен, то функция выдаёт только параметры уравнения регрессии. При этом для вывода результатов решения надо заранее выделить диапазон ячеек размером 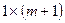, где – число факторов, включённых анализ.

– Если аргумент стат =1 (ИСТИНА), то помимо функция выдаёт дополнительную информацию об исследуемой регрессионной зависимости. В этом случае для вывода результатов решения надо выделить диапазон ячеек размером 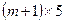. В первом столбце выделенного диапазона находятся следующие характеристики: коэффициент регрессии, стандартная ошибка коэффициента регрессии, коэффициент детерминации, расчётное значение F- критерия Фишера, сумма квадратов, обусловленная регрессией. Во втором столбце находятся значения свободного члена, его стандартная ошибка, стандартная ошибка уравнения регрессии, число степеней свободы, сумма квадратов остатков.

Так как результатом реализации функции является массив чисел, содержащий выборочные характеристики исследуемой регрессионной зависимости, то функция вводится как формула массива, то есть последовательной комбинацией клавиш Ctrl+Shift+ Enter.

Расчетное значение t – критерия Стьюдента: t=lnb/ стандартная ошибка коэффициента регрессии.

В качестве меры адекватности уравнений регрессии используется также процентное отношение стандартной ошибки к среднему уровню результативного признака 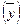– относительная ошибка аппроксимации. Если относительная ошибка 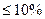, то точность модели регрессии высокая, если 10-20% – точность модели регрессии хорошая (то есть уравнение достаточно хорошо описывает взаимосвязь между изучаемыми признаками), если 20-50% – точность модели регрессии удовлетворительная.

Функции ТЕНДЕНЦИЯ и РОСТ используются для вычисления расчётных значений результативного признака, соответствующих заданным пользователем значениям факторных признаков, хранящимся в массиве новые значения х. При этом функция ТЕНДЕНЦИЯ вычисляет параметры линейной и других видов регрессии, линейных относительно входящих в них коэффициентов, таких, например, как полиноминальная регрессия, а функция РОСТ – параметры экспоненциальной регрессии. Параметры уравнений регрессий при этом не отображаются.

Задание 14.

С использованием данных листа «Множественная регрессия» по данным муниципальных районов проведите множественный корреляционно– регрессионный анализ зависимости уровня рентабельности в сельском хозяйстве региона от обеспеченности трудовыми ресурсами, оборотными средствами и основными фондами.

Осуществите оценку значимости множественного коэффициента корреляции (детерминации) и адекватности уравнения регрессии. Дайте экономическую интерпретацию уравнения регрессии.

На основе сравнения значений бета-коэффициентов регрессии и частных коэффициентов эластичности выявите, обеспеченность каким видом ресурсов является приоритетным для экономической эффективности сельского хозяйства региона.

Определите резервы роста рентабельности отрасли в регионе.

Результаты решения и выводы по ним оформите как приложение 14 к данным методическим указаниям.

Методические указания:

Множественная линейная регрессия в Excel осуществляется аналогично парной линейной регрессии. При этом в качестве исходных данных вводятся значения результативного и нескольких (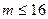) факторных признаков. Оценка значимости множественного коэффициента корреляции (детерминации) и адекватности уравнения регрессии производится аналогично порядка, описанного в задание 10.

Расчет стандартизированных коэффициентов регрессии (бета- коэффициентов) осуществляется по формуле:

;

- стандартизированный коэффициент регрессии при соответствующем факторном признаке;

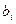- коэффициент регрессии при соответствующем факторном признаке;

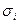- среднее квадратическое отклонение соответствующего факторного признака;

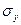-среднее квадратическое отклонение результативного признака.

Величина стандартизированных бета-коэффициентов показывает, на сколько средних квадратических отклонений 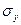изменяется у при изменении соответствующего фактора 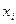на одно среднее квадратическое отклонение 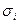при неизменности остальных факторов, входящих в уравнение регрессии.

Значения коэффициентов множественной регрессии 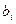находятся в третьей таблице результатов решения процедуры в графе «Коэффициенты».

Для вычисления среднего квадратического (стандартного) отклонения факторных и результативного признака применяются статистические функции СТАНДОТКЛОНП.

Расчет частных коэффициентов эластичности осуществляется по формуле:

;

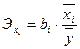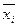-среднее значение соответствующего факторного признака;

- средне значение результативного признака;

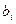- коэффициент регрессии при соответствующем факторном признаке.

Коэффициент эластичности показывает, на сколько процентов в среднем измениться значение результативного признака при измерении факторного признака на 1%.

Для выявления приоритетности влияния показателей ресурособеспеченности на рентабельность сельскохозяйственного производства осуществляется их ранжирование по величине бета-коэффициентов и частных коэффициентов эластичности:

Факторы	Значения коэффициентов	Ранг факторов по величине коэффициентов	Средний ранг
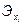
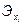
Х1
Х2
Х3

Определение резервов роста результативного показателя основывается на содержании расчетного (теоретического) уровня, определяемого путем подстановки в уравнение регрессии фактических значений факторных признаков. Расчетные уровни отражают такие уровни результативного показателя, которые были бы достигнуты при фактических значениях факторов и при средней по всей совокупности эффективности их использования.

Определение резервов роста рентабельности в регионе начинается с выявления муниципальных образований, имеющих эффективность использования ресурсов ниже средней по региону. Для этого сравнивают отклонения (остатки) у - 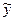фактических и расчетных (теоретических) уровней рентабельности, определяемых в процедуре Регрессия путем установки флажка Остатки. Отрицательная величина абсолютного отклонения у - 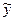свидетельствует о том, что эффективность использования ресурсов, включенных в уравнение регрессии, ниже средней эффективности их использования в регионе. Такие муниципальные образования имеют резервы, связанные с возможным повышением уровня эффективности использования ресурсов. Эти резервы могут быть связаны с достижением в этих муниципальных образованиях:

1) среднего уровня эффективности использования ресурсов в регионе;

2) уровня эффективности использования ресурсов, характерного для передовых в этом отношении муниципальных образований.

В первом случае по совокупности муниципальных образований, где фактический уровень рентабельности ниже расчетного (теоретического, предсказанного), вычисляем средний уровень показателей ресурсообеспеченност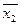и , и 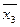. Подставляем эти уровни в построенное уравнение множественной регрессии. Тем самым получаем расчетный уровень рентабельности при условии достижения эффективности использования ресурсов в этих муниципальных образованиях среднего уровня. Разница между данным расчетным уровнем и средним фактическим уровнем рентабельности, рассчитанным для этих «отстающих» образований и будет резервом роста рентабельности.

Во втором случае выделяется группа муниципальных образований, имеющих эффективность использования ресурсов выше среднего по региону, то есть где получена положительная величина абсолютного отклонения у - .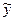

На основе первичных исходных данных по этой группе строится новая, «прогрессивная» модель регрессии. Подставив в эту модель средние значения показателей ресурсообеспечености по «отстающим» муниципальным образованиям, находится новый расчетный уровень рентабельности, сравнение которого со средним фактическим уровнем отстающих муниципальных образований и показывает величину резервов.

Поиск по сайту: