Формирование и статистическая обработка выборки

Задание 2.

1) Сформировать в столбцах массивы случайных чисел, распределенных по требуемому закону распределения, число переменных = 1, число случайных чисел = 100:

1.1. Равномерное распределение. Исходные данные min=155; max=190.

1.2. Распределение Пуассона. Исходные данные: λ = 75.

1.3. Биномиальное распределение. Исходные данные: р = 0,85; число испытаний – 100.

1.4. Нормальное распределение. Исходные данные: среднее – 1600; стандартное отклонение – 120.

2) На основе построенных в п.1.1-1.4 массивов получить случайную и периодическую выборки размером 20 элементов.

3) Для случайных выборок, полученных в п.2 рассчитать показатели анализа данных с помощью статистических функций Excel.

Результаты оформите как приложение 2 к данным методическим указаниям. Сделать выводы по результатам анализа данных.

Методические указания:

Элементы управления диалогового окна Генерация случайных чисел зависит от вида распределения, выбранного пользователем. Часть элементов управления является общими для всех распределений. К их числу относятся:

· поле ввода Число переменных. В него вводится число последовательностей случайных чисел, которые предстоит сформировать;

· поле ввода Число случайных чисел. В него вводится число случайных чисел в последовательности;

· раскрывающийся список Распределение. В списке перечислены распределения, генерируемые рассматриваемой процедурой. Нужное распределение выбирается выделением соответствующей строки списка распределений;

· поле ввода Случайное рассеивание. В это поле вводится исходное число (исходная константа) генерируемой последовательности псевдослучайных чисел. В него можно ввести любое целое число от 1 до 32 767. Заполнение этого поля необязательно– Excel сам ведет исходную констант.

Индивидуальными для каждого распределения являются поля ввода, предназначенные для установки параметров каждого из семи распределений.

Поля ввода области Параметры, соответствующие конкретным распределениям:

· равномерное распределение. Параметрами распределения являются левая и правая границы распределения. Эти параметры вводятся в поле Между…и….

· нормальное распределение. Параметры этого распределения: математическое ожидание (среднее) и стандартное отклонение;

· распределение Бернулли. Единственный параметр этого распределения –вероятность «успеха» р – вводится в поле Значение р;

· биноминальное распределение. Параметрами этого распределения являются вероятность «успеха» и число испытаний п. Они вводятся в поля Значение р и Число испытаний п (распределение Бернулли– частный случай биноминального распределения при п =1);

· распределение Пуассона. Параметром этого распределения является математическое ожидание λ пуассоновской случайной величины. Этот параметр вводится в поле Лямда;

· дискретное распределение. В поле ввода Входной интервал значений и вероятностей вводится ссылка на диапазон ячеек, содержащий ряд распределения моделируемой дискретной случайной величины. Диапазон содержит два столбца. Число строк диапазона равно числу различных возможных значений моделируемой случайной величины. В левый столбец диапазона в возрастающем порядке записываются все возможные значения случайной величины, а в правый – вероятности появления этих значений, сумма которых равна 1.

На первом этапе статистической обработки выборки используются специальные числовые параметры, найденные по результатам наблюдения и отражающие в сжатом виде основные, существенные черты распределения данных. Эти числовые параметры называются эмпирическими числовыми характеристиками. Наиболее важными числовыми характеристиками являются характеристики положения, вариации, асимметрии и эксцесса.

Для характеристики положения используются показатели центра распределения данных наблюдения – средняя арифметическая, мода и медиана. Средняя характеризует типический размер изучаемого признака. Мода распределения – это наиболее часто встречающееся значение признака в совокупности. Медиана – это значение признака, расположенное в середине (в центре) ранжированного ряда. Медиана делит совокупность на две равные части– со значениями признака меньше медианы и со значениями признака больше медианы.

Основными характеристики вариации признака являются дисперсия, стандартное отклонение, среднее линейное отклонение и коэффициент вариации. Они характеризуют степень рассеивания данных наблюдения относительно центра распределения. Абсолютные показатели вариации основаны на учете отклонений индивидуальных значений признака от средней арифметической.

Стандартное отклонение σ показывает, на сколько в среднем отклоняются индивидуальные значения признака от их средней величины. Размерность отклонения σ совпадает с размерностью самого признака. Интенсивность вариации обычно измеряют коэффициентом вариации V, который выражается в процентах и вычисляется делением стандартного отклонения на среднюю арифметическую. Для нормальных и близких к нормальному распределений показатель вариации служит индикатором однородности совокупности: принято считать, что при выполнимости неравенства V ≤ 33, % совокупность является количественно однородной по данному признаку. Коэффициент вариации V используется для сравнения колеблемости признаков в различных рядах распределения, когда сравнивается вариация разных признаков в одной и той же совокупности или же вариация одного и того же признака в различных совокупностях, имеющих разные средние x.

При резко асимметричном распределении более удобной характеристикой «центра» распределения является медиана Ме. Она более устойчива к резким выбросам данных, чем средняя, что позволяет использовать ее при работе с распределениями, имеющими «хвосты». В этом случае для измерения вариации признака применяются коэффициент вариации, определяемый делением стандартного отклонения на медиану.

Асимметрия характеризует меру несимметричности (скошенности) распределения. Если коэффициент асимметрии больше нуля, то асимметрия правосторонняя, если меньше нуля – левосторонняя. Выборочный коэффициент асимметрии, основанный на определении центрального момента третьего порядка (в нормальном распределении его величина равна нулю): . В Excel вычисляется несмещённая состоятельная оценка коэффициента асимметрии:

, .

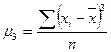Стандартизированный коэффициент асимметрии имеет приближённое стандартное нормальное распределение.

Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения, имеющей куполообразную форму. Эксцесс характеризует островершинность (плосковершинность) распределения. Если эксцесс больше нуля, то распределение островершинное, если меньше нуля – плосковершинное. В Excel вычисляется несмещённая состоятельная оценка коэффициента. Наиболее точным является выборочный коэффициент эксцесса, основанный на использовании центрального момента четвёртого порядка: . Для нормального распределения 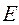равен нулю, так как 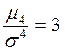. В Excel вычисляется несмещённая состоятельная оценка коэффициента:

; .

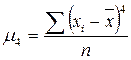Стандартизированный выборочный коэффициент эксцесса 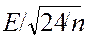используется при оценке степени отклонения распределения исследуемой случайной величины от нормального распределения.

В Excel числовые характеристики вычисляются с помощью соответствующих встроенных статистических функций СРЗНАЧ, МЕДИАНА, МОДА, ДИСП, ДИСП, СТАНДОТКЛОН, СРОТКЛ, КВАДРОТКЛ, СКОС и ЭКСЦЕСС.

Задание 3.

Посредством статистической процедуры Пакета анализа Excel Описательная статистика вычислите числовые характеристики распределения поставщиков по продолжительности договорных связей поставщиком с магазином и по фактическому объему поставки.

Сделайте предположения о принадлежности данных распределений к нормальному распределению на основе: а) сравнения показателей центра распределения; б ) на основе стандартизированных значений показателей асимметрии и эксцесса по формулам и 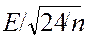: при нормальном распределении при уровне вероятности 95% их значения должны находиться в пределах (-1,96; 1,96).

Сравните степень вариации двух признаков.

Результаты оформите как приложение 3 к данным методическим указаниям (в формате Документ Microsoft Office Word).

Методические указания:

Для доступа к процедуре Описательная статистика необходимо:

В окне Анализ данных выделить процедуру Описательная статистика и щёлкнуть на кнопке ОК. На экране появится диалоговое окно Описательная статистика, которое содержит следующие элементы управления:

· поле ввода Входной интервал. В это поле вводится ссылка на диапазон ячеек (входной диапазон), содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом или группой смежных столбцов (строкой или группой смежных строк). Если входной диапазон представляет собой группу столбцов (строк), то процедура воспринимает каждый столбец (строку) как отдельную совокупность;

· флажок Итоговая статистика. Если этот флажок установлен, процедура вычисляет и помещает в таблицу результатов решения следующие числовые характеристики: среднюю, стандартную ошибку средней, медиану, моду, стандартное отклонение, дисперсию, эксцесс, асимметрию, размах вариации, минимальное и максимальное значение изучаемого признака, сумму всех значений признака и объём совокупности. Если совокупность не имеет повторяющихся значений признака, в строке Мода появляется сообщение # Н/Д! – неопределённые данные;

· флажок Уровень надёжности. Флажок устанавливается в том случае, когда необходимо вычислить доверительный интервал для средней, соответствующий заданной доверительной вероятности. При этом справа от флажка открывается поле для ввода доверительной вероятности, выраженной в процентах. Если этот флажок установлен, то в последней строке таблицы результатов решения появляется число, равное половине длины доверительного интервала;

· флажки К-й наименьший/К-й наибольший. Если эти флажки установлены. то в таблице результатов решения появляются -й и -й элементы упорядоченной совокупности (то есть единицы совокупности, расположенные на -м месте от её начала и от конца).

Результаты решения выводятся на экран в виде набора таблиц– по одной таблице на каждый столбец входного интервала (на каждую обработанную совокупность). Каждая выходная таблица состоит из двух столбцов. В первом столбце указывается названия числовых характеристик, во втором– их значения. В заголовке указывается номер совокупности, к которой относится данная таблица (например, Столбец 1).

Свой наибольший размер (18×2) таблица принимает при установке всех четырёх флажков, расположенных в нижней части диалогового окна процедуры. В случае возникновения опасности того, что таблица результатов наложится на уже заполненные ячейки, на экран выводится сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых (для этого надо щёлкнуть на кнопке ОК).

В тех случаях, когда форма распределения анализируется на ее близость к нормальной форме, расхождение между ними оценивается показателями асимметрии и эксцесса. Показатели асимметрии оценивают смещение ряда распределения влево или вправо по отношению к оси симметрии нормального распределения. В симметричном распределении максимальная ордината прямой располагается точно в середине кривой, а соответствующие ей характеристики центра распределения совпадают:

x = Мо = Me.

а) правосторонняя асимметрия б) левосторонняя асимметрия

Рис.1. Кривые асимметричных распределений (пунктиром обозначена нормальная кривая)

В случае асимметричного распределения вершина кривой находится не в середине, а сдвинута либо влево, либо вправо (см.рис.1). Если вершина сдвинута влево, то правая часть кривой оказывается длиннее левой (рис 1.,а), т.е. имеет место правосторонняя асимметрия, характеризующаяся неравенством х > Ме >. Если же вершина кривой сдвинута вправо и левая часть оказывается длиннее правой, то асимметрия левосторонняя (рис.1,б), для которой справедливо неравенство х < Me < Мо.

Чем больше величина расхождения между х, Me, Mo, тем более асимметричен ряд.

Чем больше величина коэффициента асимметрии As, тем более асимметрично распределение. Установлена следующая оценочная шкала асимметричности:

– As ≤ 0,25 – асимметрия незначительная;

– 0,25< As ≤ 0,5 – асимметрия заметная (умеренная);

– As >0,5 – асимметрия существенная.

Показатель эксцесса характеризует крутизну кривой распределения – ее заостренность или пологость по сравнению с нормальной кривой (рис.2).

а) островершинное распределение б) плосковершинное распределение

Рис.2. Кривые распределения с ненулевым эксцессом (пунктиром обозначена нормальная кривая)

Относительно вершины нормальной кривой и определяется выпад вверх или вниз вершины теоретической кривой эмпирического распределения. При этом:

– если E >0, то вершина кривой распределения располагается выше вершины нормальной кривой, а форма кривой является более островершинной, чем нормальная (рис. 2,а). Это говорит о скоплении значений признака в центральной зоне ряда распределения, т.е. о преимущественном появлении в данных значений, близких к средним;

– если E < 0, то вершина кривой распределения лежит ниже вершины нормальной кривой, а форма кривой более пологая по сравнению с нормальной (рис. 2,б). Это означает, что значения признака не концентрируются в центральной части ряда, а достаточно равномерно рассеяны по всему диапазону от x max до x min.

Для нормального распределения Ek = 0, поэтому чем больше абсолютная величина | Ek |, тем существеннее распределение отличается от нормального.

Сравнение вариации разных признаков производится на основе значений коэффициента вариации, определяемого как отношение стандартного отклонения к средней арифметической и выражаемого в процентах.

Задание 4.

Произведите 10-% собственно-случайную и механическую (периодическую) выборку из 100 поставщиков магазина. По данным выборки определите средний размер объема поставок товаров магазину всеми поставщиками, гарантируя результат с вероятностью 0,95.

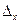Для этого с помощью процедуры Описательная статистика или статистической функции ДОВЕРИТ постройте доверительный интервал , где -выборочная средняя; - предельная ошибка выборки.

Аналогичный расчет произведите на основе формул. Для этого по выборочной совокупности с помощью статистической функции СРЗНАЧ рассчитайте средний объем поставок товаров магазину . Вычислите предельную ошибку выборки для средней по формуле , где

– - критерий Стьюдента (находится с помощью статистической функции СТЬЮДРАСПОБР при уровне значимости α =0,05 и числе степеней свободы );

– выборочная дисперсия (находится с помощью статистической функции ДИСП);

– -объем выборочной совокупности.

Сравните результаты собственно-случайной и механической выборки.

Результаты выборочного наблюдения и выводы по ним оформите как приложение 4 к данным методическим указаниям (в формате Документ Microsoft Office Word).

Методические указания:

В Пакете анализа табличного процессора Excel имеется процедура Выборка, реализующая повторную собственно-случайную выборку и механическую выборку с заданным пользователем шагом (периодом) отбора.

Формирование выборки в Excel осуществляется следующим образом:

1. Единицам генеральной совокупности присваиваются порядковые номера. Для проведения механической выборки генеральная совокупность должна быть каким-либо образом упорядочена, то есть должна быть определённая последовательность в расположении её единиц. Для получения результатов, не содержащих систематическую ошибку выборки, упорядочение необходимо произвести по нейтральному признаку по отношению к изучаемому.

2. Порядковые номера единиц исходной совокупности вводятся в диапазон ячеек (входной диапазон). Эти номера могут находиться в одном столбце или группе смежных столбцов одинаковой «высоты». При этом число всех ячеек входного диапазона должно равняться числу единиц исходной совокупности. Если среди элементов входного интервала имеются нечисловые данные, то отбор не состоится, а на экране появится сообщение «Выборка– входной интервал содержит нечисловые данные».

3. В диалоговом окне Анализ данных выделяется процедура Выборка и нажимается кнопка ОК. На экране появится диалоговое окно Выборка, которое содержит следующие элементы управления:

· поле ввода Входной интервал. В это поле вводится ссылка на диапазон, в котором хранятся номера всех единиц генеральной совокупности, из которой осуществляется выборка.

· Метод выборки устанавливается с помощью переключателей Периодический и Случайный. При активизации переключателя Случайный процедура «настраивается» на выполнение собственно-случайной выборки с повторением. Нужный объём выборки вводится в поле Число выборок. Единицы генеральной совокупности отбираются случайным образом. Каждая единица исходной совокупности имеет равную со всеми остальными единицами возможность быть включённой в выборку. Любая единица генеральной совокупности может попасть в выборку более одного раза.

При необходимости реализовать механическую выборку активизируется переключатель Периодический. Шаг выборки вводится в поле Период, находящееся справа от переключателя. В выборку войдут элементы исходной совокупности с номерами, кратными заданному периоду. Если входной диапазон состоит из нескольких столбцов, то отбираемые значения будут извлекаться сначала из первого столбца, затем из второго и т.д. Формирование выборки прекращается по достижении конца исходной совокупности.

При формировании случайной выборки выходной интервал представляет собой столбец с числом ячеек, равным заданному объёму выборки. В случае механической выборки число ячеек выходного интервала равно целой части результата деления объёма исходной совокупности на шаг выборки.

Для получения упорядоченной копии номеров единиц совокупности, подлежащих включению в выборку, необходимо щелчком на кнопке Сортировка по возрастанию, расположенной на панели инструментов Стандартная, упорядочить полученный набор номеров.

По каждому поставщику записывается объем поставки товаров. По сформированной выборке вычисляются эмпирические числовые характеристики с помощью статистической процедуры Описательная статистика, в которой устанавливается флажок Уровень надежности. В поле ввода задается доверительная вероятность, выраженной в процентах (по умолчанию 95%). В последней строке таблицы результатов решения появляется число, равное половине длины доверительного интервала, то есть предельная ошибка выборки.

Функция ДОВЕРИТ вычисляет полуширину доверительного интервала средней(предельной ошибки выборки) по заданному уровню значимости, стандартному отклонению и числу значений в выборке.

Задание 5.

Произведите собственно-случайную выборку 35 сельскохозяйственных предприятий с целью изучения среднего уровня заработной платы в сельском хозяйстве региона и доли прибыльных предприятий. При определении доверительного интервала доли предприятий (альтернативного признака) используется формула: 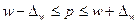, где

w - доля предприятий с положительным финансовым результатом (прибылью) в выборочной совокупности;

m - число прибыльных предприятий;

n – объем выборки;

Отбор из базы данных отдельных записей (прибыльных предприятий) можно осуществить по условиям фильтра. Для этого предварительно необходимо изменить цвет ячеек прибыльных предприятий. Далее нужно установить курсор на любой ячейке списка и включить фильтрацию с помощью команды: Данные®Фильтр® (правой кнопкой мыши) Фильтр по цвету выделенной ячейки.

В результате база данных будет отфильтрована, и в списке останутся только записи, соответствующие заданному критерию (записи прибыльных предприятий). Теперь с помощью статистической функции СЧЕТ нужно подсчитать количество прибыльных предприятий. После окончания анализа необходимо отменить действие фильтра.

- предельная ошибка выборки для доли; .

Результаты выборочного наблюдения и выводы по ним оформите как приложение 5 к данным методическим указаниям.

Поиск по сайту: