 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РАСЧЕТ ПОКАЗАТЕЛЕЙ КОРРЕЛЯЦИИ
Цель – познакомить студентов с основными способами расчета показателей корреляции.
В отличие от функциональной связи, когда одному значению аргумента (х) соответствует определенное значение функции (у), при корреляционной связи – одному конкретному значению аргумента соответствует приближенное, или некоторое множество значений функции. Близость этого множества значений функции к друг другу соответствует понятию силы или тесноты корреляционной связи.
Биологические объекты всегда в той или иной степени неоднородны по своим наследственным особенностям и, кроме того, в любом, даже тщательно спланированном эксперименте его объекты испытывают не учитываемые воздействия факторов внешней среды.
При изучении корреляционных связей возникают два основных вопроса – о тесноте связи и о форме связи. Для измерения тесноты и формы связи используют специальные статистические методы, называемые корреляцией и регрессией. По форме корреляция может быть линейной и криволинейной, по направлению прямой и обратной. В пособии рассматривается только случай линейной корреляции как наиболее простой.
Под линейной корреляцией между двумя признаками X и Y понимают такую зависимость, которая носит линейный характер и выражается уравнением прямой линии Y = a + bX. Это уравнение называется уравнением регрессии Y по X, а соответствующая ему прямая линия – выборочной линией регрессии.
Пример 5.1. Изучали зависимость между массой тела гамадрилов-матерей и их новорожденных детенышей. Под наблюдением находилось 20 обезьян. Результаты наблюдений приведены в первых двух столбцах таблицы.
Масса тела матерей 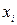 , кг , кг
| Масса тела детенышей  , кг , кг
| 
| 
| 
|
| 10,0 | 0,70 | – 1,87 | ||
| 10,8 | 0,73 | –1,07 | 0,03 | –0,0320 |
| 11,3 | 0,75 | –0,57 | 0,05 | –0,0285 |
| 10,0 | 0,70 | –1,87 | ||
| 10,1 | 0,65 | –1,77 | –0,05 | 0,0885 |
| 11,1 | 0,65 | –0,77 | –0,05 | 0,0385 |
| 11,3 | 0,70 | –0,57 | ||
| 10,2 | 0,61 | –1,67 | –0,09 | 0,1503 |
| 13,5 | 0,70 | 1,63 | ||
| 12,3 | 0,63 | 0,43 | –0,07 | –0,0301 |
| 14,5 | 0,70 | 2,63 | ||
| 11,0 | 0,65 | –0,87 | –0,05 | 0,0435 |
| 12,0 | 0,72 | 0,13 | 0,02 | 0,0026 |
| 11,8 | 0,69 | –0,07 | –0,01 | 0,0070 |
| 13,4 | 0,78 | 1,53 | 0,08 | 0,1224 |
| 11,4 | 0,70 | –0,47 | ||
| 12,0 | 0,60 | 0,13 | –0,10 | –0,0130 |
| 15,6 | 0,85 | 3,73 | 0,15 | 0,5595 |
| 13,0 | 0,80 | 1.13 | 0,10 | 0,1130 |
| 12,1 | 0,75 | 0,23 | 0,05 | 0,0115 |
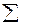 = 237,4 = 237,4
| 14,06 | +1,0332 |
Необходимо установить тесноту и направление связи между этими признаками.
Для этого наиболее приемлемой статистикой является коэффициент корреляции, который вычисляется по формуле:

Коэффициент вариации это отвлеченное число, лежащее в интервалах от – 1 до + 1. При независимом варьировании признаков, когда связь между ними полностью отсутствует,  = 0. Чем сильнее сопряженность между признаками, тем выше значение коэффициента корреляции. При положительной или прямой связи, когда большим значениям одного признака соответствует большее же значение другого, коэффициент корреляции имеет положительный знак, при отрицательной или обратной связи, когда большим значениям одного признака соответствуют меньшие значения другого, коэффициент корреляции сопровождается отрицательным знаком.
= 0. Чем сильнее сопряженность между признаками, тем выше значение коэффициента корреляции. При положительной или прямой связи, когда большим значениям одного признака соответствует большее же значение другого, коэффициент корреляции имеет положительный знак, при отрицательной или обратной связи, когда большим значениям одного признака соответствуют меньшие значения другого, коэффициент корреляции сопровождается отрицательным знаком.
Для расчета коэффициента корреляции нам необходимо найти значения средних арифметических для анализируемой пары признаков. Они равны  = 11,87 и
= 11,87 и  = 0,70.
= 0,70.
Далее находим значения средних квадратических отклонений, по формулам известным из предыдущих модулей задачника. Они равны  = 1,516 и
= 1,516 и  = 0,063.
= 0,063.
Рассчитаем значение  . Оно равно + 1,0332. Подставим полученные промежуточные статистики в формулу:
. Оно равно + 1,0332. Подставим полученные промежуточные статистики в формулу:

Таким образом, полученная величина эмпирического коэффициента вариации указывает на наличие положительной средней силы корреляционной связи между массой тела гамадрилов матерей и массой тела их детенышей.
Эмпирический коэффициент корреляции служит оценкой своего генерального параметра (генерального коэффициента корреляции  ) и как величина случайная сопровождается ошибкой:
) и как величина случайная сопровождается ошибкой:
 =
=  0,198
0,198
Отношение выборочного коэффициента корреляции к своей ошибке служит критерием для проверки нулевой гипотезы – предположения, что в генеральной совокупности этот показатель равен нулю, т.е.  = 0. Нулевую гипотезу отвергают на принятом уровне доверительной вероятности, если:
= 0. Нулевую гипотезу отвергают на принятом уровне доверительной вероятности, если:

Рассчитаем фактический критерий Стьюдента:
 .
.
По таблице значений критерия Стьюдента находим  при k = 20 –1 = 18 и P = 95%, который равен 2,10.
при k = 20 –1 = 18 и P = 95%, который равен 2,10.
Таким образом, нулевая гипотеза отвергается при доверительной вероятности P = 95%.
После того как установлено наличие корреляционной связи между двумя изученными признаками, можно установить закономерность количественного изменения одного из признаков (функция) при изменении другого (аргумент). С этой целью изучаемую связь выражают аналитически – в виде соответствующего уравнения регрессии и графически – с вычислением точек теоретической кривой по найденному уравнению.
Пример 5.2. Необходимо рассчитать уравнение линейной регрессии отражающую зависимость между массой тела гамадрилов-матерей и их новорожденных детенышей и выразить его графически (по данным примера 5.1.).
Уравнение регрессии может быть записано следующим образом:
 и
и  , где
, где 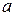 – свободный член уравнения, b – коэффициент регрессии, определяющий наклон линии регрессии по отношению к осям прямоугольных координат. Коэффициент регрессии показывает, насколько в среднем величина одного признака изменяется на единицу меры другого. Этот показатель определяется по формуле:
– свободный член уравнения, b – коэффициент регрессии, определяющий наклон линии регрессии по отношению к осям прямоугольных координат. Коэффициент регрессии показывает, насколько в среднем величина одного признака изменяется на единицу меры другого. Этот показатель определяется по формуле:  или
или  .
.
Найдем значение  .
.
Используя уравнение  , найдем значение
, найдем значение  , подставив в формулу ранее найденные значения средних арифметических обоих признаков и значение коэффициента регрессии:
, подставив в формулу ранее найденные значения средних арифметических обоих признаков и значение коэффициента регрессии:  откуда
откуда  = 0,70 – 0,267 = 0,433
= 0,70 – 0,267 = 0,433
В результате уравнение регрессии будет выглядеть следующим образом: 

Графическое выражение рассчитанной регрессии представлено на рисунке.
На рисунке прямая – теоретическая линия прямолинейной регрессии расположена на фоне эмпирических значений функции.
Ошибка уравнения прямолинейной регрессии (ли криволинейной) вычисляется по формуле:  , где y – эмпирическое значение функции;
, где y – эмпирическое значение функции;  – теоретическое значение функции; n – число точек эмпирической линии регрессии; k – число коэффициентов уравнения, включая свободный член (для линейной регрессии 2).
– теоретическое значение функции; n – число точек эмпирической линии регрессии; k – число коэффициентов уравнения, включая свободный член (для линейной регрессии 2).
Необходимые для определения ошибки регрессии, предварительные расчеты приведены в таблице
Масса тела матерей 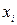
| Масса тела детенышей 
| Теоретические значения функции 
| 
|
| 10,0 | 0,70 | 0,658 | 0,002 |
| 10,8 | 0,73 | 0,676 | 0,003 |
| 11,3 | 0,75 | 0,687 | 0,004 |
| 10,0 | 0,70 | 0,658 | 0,002 |
| 10,1 | 0,65 | 0,660 | 0,0001 |
| 11,1 | 0,65 | 0,683 | 0,001 |
| 11,3 | 0,70 | 0,687 | 0,0003 |
| 10,2 | 0,61 | 0,663 | 0,003 |
| 13,5 | 0,70 | 0,737 | 0,001 |
| 12,3 | 0,63 | 0,710 | 0,006 |
| 14,5 | 0,70 | 0,759 | 0,004 |
| 11,0 | 0,65 | 0,681 | 0,001 |
| 12,0 | 0,72 | 0,703 | 0,0003 |
| 11,8 | 0,69 | 0,699 | 0,0001 |
| 13,4 | 0,78 | 0,735 | 0,002 |
| 11,4 | 0,70 | 0,690 | 0,0001 |
| 12,0 | 0,60 | 0,703 | 0,011 |
| 15,6 | 0,85 | 0,784 | 0,066 |
| 13,0 | 0,80 | 0,726 | 0,0006 |
| 12,1 | 0,75 | 0,705 | 0,002 |
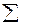
| 0,1115 |
Подставим полученные результаты в формулу  .
.
Коэффициент регрессии – основной параметр уравнения прямой линии, поэтому необходимо оценивать достоверность отличия коэффициента b от нуля ( : b = 0).
: b = 0).
Критерий Стьюдента рассчитывается по формуле:
 , где
, где  – коэффициент при аргументе в уравнении прямой линии;
– коэффициент при аргументе в уравнении прямой линии;  – среднее квадратическое отклонение ряда аргумента;
– среднее квадратическое отклонение ряда аргумента;  – ошибка уравнения регрессии; n – объем выборки (количество пар).
– ошибка уравнения регрессии; n – объем выборки (количество пар).
Фактическое значение коэффициента Стьюдента 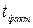 сравнивается с
сравнивается с  при числе степеней свободы k = n – 2; если вычисленная величина больше табличной, то связь между x, y и значение
при числе степеней свободы k = n – 2; если вычисленная величина больше табличной, то связь между x, y и значение  достоверны, а если вычисленная меньше табличной величины, то связь данных признаков и значение
достоверны, а если вычисленная меньше табличной величины, то связь данных признаков и значение  недостоверны. Для данного примера
недостоверны. Для данного примера

По таблице при P = 95%  = 2,093, так как
= 2,093, так как 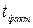
 , нулевая гипотеза остается в силе. Действительно, для таких экспериментов выборка объемом 20 объектов является недостаточной.
, нулевая гипотеза остается в силе. Действительно, для таких экспериментов выборка объемом 20 объектов является недостаточной.
Пример 5.3. Требуется объективно подобрать из числа опытных специалистов группу экспертов для оценки сортов декоративных растений. Для этого двум специалистам предлагается оценить 13 сортов одной цветочной культуры. Оценка ведется по комплексу признаков и выражается в виде суммы балов.
В этом случае может быть использован показатель корреляции рангов по Спирмэну. Сила корреляционной связи между двумя признаками при помощи этого показателя измеряется в основном для небольших невзвешенных рядов, которые представляют собой качественные оценки признаков.
Необходимые данные для расчета показателя корреляции рангов между оценками двух экспертов приведены в таблице.
| Сумма баллов первого эксперта, х | Сумма баллов второго эксперта, у | Ранг, х | Ранг, у | Разность рангов,  
| 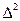
|
| 3,5 | 3,5 | ||||
| 3,5 | 2,5 | 6,25 | |||
| 8,5 | 2,5 | 6,25 | |||
| 8,5 | 1,5 | 2,25 | |||
| 3,5 | 7,5 | 56,25 | |||
 Показатель корреляции рангов по Спирмэну рассчитывается по формуле:
Показатель корреляции рангов по Спирмэну рассчитывается по формуле:
 , где n – число пар вариант корреляционных рядов,
, где n – число пар вариант корреляционных рядов,  – сумма квадратов попарных разностей рангов.
– сумма квадратов попарных разностей рангов.
Последовательность действий при расчете показателя корреляции рангов следующая:
Ранжируем данные рядов Х и У от большего к меньшему, присваивая вариантам порядковый номер. Варианта 72 ряда Х получает ранг 1, варианта 67 – ранг 2, варианты 64 и 64 должны были бы получить ранги 3 и 4, но так как они имеют равное значение, то берется средний ранг для обеих вариант: (3+4)/2 = 3,5. Остальные ранги рядов присваиваются по аналогии и представлены в таблице;
Получаем разность рангов без учета их знаков;
Возводим разности в квадрат и суммируем, получаем  = 479;
= 479;
Подставляем полученные значения в формулу
 = – 0,32.
= – 0,32.
Достоверность показателя корреляции рангов оценивается по формуле
 .
.
Подставим имеющиеся данные и найдем  . При Р = 95% и k = n -- 2 = 13 – 2 = 11,
. При Р = 95% и k = n -- 2 = 13 – 2 = 11,  =2,201.
=2,201.
Следовательно, полученный показатель корреляции рангов статистически недостоверен и кандидаты на должность эксперта не подходят или не подходит один из них.
Пример 5.4. Необходимо установить связь между плодовитостью самок кролика в системе «родители – дети»
| Число детенышей в помете у «матерей», х | Число детенышей в помете у «дочерей», у | Ранг, х | Ранг, у | Разность рангов,  
| 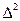
|
В этом случае показатель наследуемости может служить коэффициент корреляции рангов Спирмэна, способ расчета которого приведен в примере 5.3.
Подставим имеющиеся значения в формулу:  =
=  = +0,80. Полученный коэффициент указывает на тесную и прямую зависимость между плодовитостью «матерей» и «дочерей».
= +0,80. Полученный коэффициент указывает на тесную и прямую зависимость между плодовитостью «матерей» и «дочерей».
Достоверность показателя наследуемости (корреляции рангов) оценим по формуле  . Подставим имеющиеся данные и найдем
. Подставим имеющиеся данные и найдем  . При Р = 95% и k = n – 2 = 5 – 2 = 3,
. При Р = 95% и k = n – 2 = 5 – 2 = 3,  = 3,182. Так как,
= 3,182. Так как, 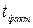 >
>  , нулевая гипотеза отвергается и связь между плодовитостью «матерей» и «дочерей» считается статистически доказанной.
, нулевая гипотеза отвергается и связь между плодовитостью «матерей» и «дочерей» считается статистически доказанной.
Вопросы для самоконтроля:
1. Что такое корреляция?
2. Какая разница между корреляционной и функциональной зависимостью?
3. Какая разница между положительной и отрицательной корреляциями?
4. Что такое корреляционная решетка? Объясните как она строится. Можно ли судить о характере корреляции по расположению данных в корреляционной решетке?
5. Каковы возможные значения коэффициента корреляции? Какие значения коэффициента корреляции следует считать высокими, средними и почему?
6. Всегда ли при r = 0 корреляционная связь отсутствует?
7. Чему равен коэффициент корреляции при полной корреляционной связи?
Поиск по сайту: