 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Показатели варьирования (разнообразия)
В биологии используются несколько показателей разнообразия. Самыми простыми из них являются лимиты (lim) и размах варьирования (R). Лимиты и размах определяются без вычислений по следующим простым формулам:
lim = 
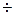

 и R =
и R =  –
–  , где
, где  и
и  наименьшая и наибольшая дата статистической совокупности. Так для задачи с определением продолжительности вегетационного периода у сортов ячменя (пример 1.1.) lim = 60
наименьшая и наибольшая дата статистической совокупности. Так для задачи с определением продолжительности вегетационного периода у сортов ячменя (пример 1.1.) lim = 60 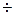 90, а R = 92–60 = 32.
90, а R = 92–60 = 32.
Однако наиболее широкое использование в исследованиях получили среднее квадратическое отклонение (σ) или сигма и дисперсия – среднее квадратическое отклонение в квадрате (σ  ). Среднее квадратическое отклонение и дисперсия оценивают величину колебаний значений вариант около их средней арифметической и служат кроме того для расчета других биометрических показателей.
). Среднее квадратическое отклонение и дисперсия оценивают величину колебаний значений вариант около их средней арифметической и служат кроме того для расчета других биометрических показателей.
Среднее квадратическое отклонение вычисляется по формуле
σ = + 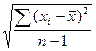 , где σ – среднее квадратическое отклонение;
, где σ – среднее квадратическое отклонение; 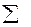 – знак суммирования;
– знак суммирования; 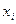 – варианты (даты) совокупности;
– варианты (даты) совокупности;  – средняя арифметическая; n – объем выборки.
– средняя арифметическая; n – объем выборки.
Пример 2.7. Необходимо рассчитать варьирование растений сои по высоте (данные из примера 2.1).
Вычисление сигмы по приведенной формуле проводится в следующем порядке.
1. Определяется средняя арифметическая. Для данного ряда она вычеслена в примере 1. и равна  = 64,538.
= 64,538.
2. Находится отклонение вариант путем вычисления от каждой из них средней арифметической: 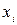 –
–  . Вычитая: 82–64,538 = 17, 462: 77 – 64,538 и т.д. (см. таблицу). Сумма всех разностей должна быть равна нулю.
. Вычитая: 82–64,538 = 17, 462: 77 – 64,538 и т.д. (см. таблицу). Сумма всех разностей должна быть равна нулю.
3. Возводятся в квадрат отклонения и получается их сумма:
 = 1721, 231.
= 1721, 231.
4. Вычисляется сигма по формуле:
σ = + 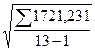 = 11,98.
= 11,98.
Варианта, 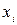
| 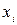 – – 
| 
|
| 17,462 | 304,921 | |
| 12,462 | 155,301 | |
| 9,462 | 89,529 | |
| 9,462 | 89,529 | |
| 8,462 | 71,605 | |
| 1,462 | 2,137 | |
| -0,538 | 0,289 | |
| -1,538 | 2,365 | |
| -1,538 | 2,365 | |
| -2,538 | 6,441 | |
| -10,538 | 111,049 | |
| -20,538 | 421,809 | |
| -21,538 | 463,885 | |
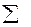
| 0,006 | 1721,231 |
В промежуточных вычислениях показателей обычно сохраняется число знаков, достаточное для получения необходимой точности, сам же показатель приводится в результате с числом знаков, имеющим реальное значение, т.е. среднее квадратическое отклонение высоты сои равно 12 см. Дисперсия этого признака (σ  ) равна144 (в отличии от среднего квадратического отклонения дисперсия это статистика не поименованная),
) равна144 (в отличии от среднего квадратического отклонения дисперсия это статистика не поименованная),
lim = 43 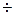 82, а R = 39.
82, а R = 39.
Пример 2.8. Известны средние арифметические и средние квадратические отклонения для массы тела и длины ног домашней и дикой птицы. Необходимо объективно сравнить изменчивость этих признаков у двух выборочных совокупностей.
| Объект | Признак | Варьирование, σ | Средняя арифметическая, 
| Коэффициент вариации – Cv, % |
| Куры | Длина ног | 1 см | 10 см | 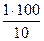 = 10% = 10%
|
| Масса тела | 0,6 кг | 3 кг | 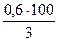 = 20% = 20%
| |
| Страусы | Длина ног | 6 см | 150 см | 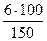 = 4% = 4%
|
| Масса тела | 10 кг | 100 кг |  = 10% = 10%
|
Среднее квадратическое отклонение и дисперсия могут служить для сравнения разнообразия статистических совокупностей только при соблюдении следующих условий:
1. При сравнении одинаковых признаков;
2. Если средние сравниваемых статистических совокупностей не очень сильно различаются.
В противном случае используются не абсолютные, а относительные показатели вариации, среди которых наиболее применяемый – коэффициент вариации (Cv). Он вычисляется по формуле:
Cv = 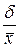 100% и представляет собой среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической.
100% и представляет собой среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической.
Действительно по величине сигмы невозможно установить, какой признак более разнообразен: нельзя сравнить 1 см длины ног с 0,6 кг массы или 6 см длины с 10 кг массы. Кроме того, 1 см для мелкой птицы несравним с 6 см для крупной. Это затруднение при решении задачи снято с помощью коэффициента вариации: у домашней птицы признаки более разнообразны по сравнению с дикой птицей, для которой сказывается действие стабилизирующего отбора. Длина ног имеет явно меньшее разнообразие по сравнению с разнообразием массы, у кур это связано с отсутствием селекции по длине ног, у страусов сказывается более жесткий стабилизирующий отбор.
Варьирование считается слабым, если коэффициент вариации не превышает 10%, средним, когда он составляет 11…25%, и значительным при Cv > 25%.
Пример 2.9. Необходимо вычислить среднюю дисперсию для четырех групп измерений диаметра цветков гелениума осеннего по данным таблицы
| Группа | Дисперсия диаметра цветка, мм | Объем выборки |
| 2,00 | ||
| 3,35 | ||
| 2,95 | ||
| 4,37 |
В примере 2.4. было показано, как объединить выборки по их средним арифметическим. Часто при этом требуется также найти и среднюю дисперсию объединенной выборки. Она может быть рассчитана по формуле:
σ  =
= 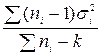 , где σ
, где σ 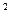 – средняя дисперсия; σ
– средняя дисперсия; σ 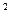
 – дисперсии частных выборок;
– дисперсии частных выборок;  – объемы частных выборок; k – число частных выборок.
– объемы частных выборок; k – число частных выборок.
По выше приведенной формуле
σ  =
= 
Поиск по сайту: