 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
СРАВНЕНИЕ ВЫБОРОК И СТАТИСТИЧЕСКИХ ПАРАМЕТРОВ
Цель – познакомить студентов с некоторыми статистическими методами проверки нулевой гипотезы (Н0).
В биологии часто возникает необходимость провести сравнение генеральных параметров различных совокупностей по разности, наблюдаемой между сравниваемыми выборками. О преимуществе той или иной из сопоставляемых совокупностей судят по разности между средними долями и другими выборочными показателями. В области биометрии широкое применение получила так называемая нулевая гипотеза (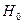 ). Сущность ее сводится к предположению, что разница между генеральными параметрами сравниваемых групп равна нулю и имеющиеся различия носят не систематический, а случайный характер. Существует ряд статистических методов для проверки принятой гипотезы.
). Сущность ее сводится к предположению, что разница между генеральными параметрами сравниваемых групп равна нулю и имеющиеся различия носят не систематический, а случайный характер. Существует ряд статистических методов для проверки принятой гипотезы.
Пример 4.1. Сравнивали массу взрослых индеек двух пород после одинакового откорма. По выборкам получены следующие сводные показатели:
| Группа | Объем выборки, n | Средняя арифметическая 
| Дисперсия 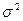
|
| Порода 1 | 4,0 ± 0,3 | 1,8 | |
| Порода 2 | 4,6 ± 0,4 | 3,2 |
Требуется установить, является ли наблюдаемые различия статистически достоверными или, нося случайный характер, т.е. сравнить генеральные параметры совокупностей.
Решение задачи необходимо начинать со сравнения генеральных дисперсий, так как в зависимости от того равны они или нет используются разные подходы для сравнения генеральных средних.
Выдвигаем нулевую гипотезу 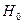 :
: 
Выбираем уровень доверительной вероятности P = 95%
Сравнение дисперсий производим следующим образом: 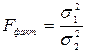 , где F критерий Фишера. За
, где F критерий Фишера. За  всегда берется большее значение, т.е. критерий Фишера не может быть меньше единицы. Рассчитываем фактический критерий Фишера
всегда берется большее значение, т.е. критерий Фишера не может быть меньше единицы. Рассчитываем фактический критерий Фишера  .
.
Находим для каждой дисперсии число степеней свободы:  = 20 – 1= 19;
= 20 – 1= 19; 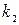 = 20–1 =19. По таблице «Значение критерия F при различных доверительных уровнях» находим значение стандартного критерия Фишера
= 20–1 =19. По таблице «Значение критерия F при различных доверительных уровнях» находим значение стандартного критерия Фишера  , которое равно 2,21. Если
, которое равно 2,21. Если 
 >
>  , то нулевая гипотеза остается в силе, в случае когда
, то нулевая гипотеза остается в силе, в случае когда 
 <
<  опровергается. Так как 2,21 больше, чем 1,78 испытанные породы индюшек по изменчивости массы достоверно не различаются при P = 95% (вернее сказать, что разность между изменчивостью массы индюшек статистически не доказана).
опровергается. Так как 2,21 больше, чем 1,78 испытанные породы индюшек по изменчивости массы достоверно не различаются при P = 95% (вернее сказать, что разность между изменчивостью массы индюшек статистически не доказана).
Далее переходим к сравнению средних арифметических.
Выдвигаем нулевую гипотезу 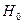 :
:  .
.
Достоверность разности между выборочными средними оценивается с помощью критерия Стьюдента по формуле:
 , где
, где 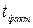 – фактический критерий Стьюдента;
– фактический критерий Стьюдента;  и
и 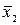 – сравниваемы выборочные средние арифметические;
– сравниваемы выборочные средние арифметические;  и
и 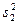 возведенные в квадрат статистически ошибки средних арифметических. Подставим имеющиеся значения в формулу. Получаем, что
возведенные в квадрат статистически ошибки средних арифметических. Подставим имеющиеся значения в формулу. Получаем, что

Находим число степеней свободы для определения стандартного значения критерия Фишера, которое вычисляется по формуле k = 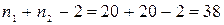 . По таблице «Значения критерия Стьюдента» при P = 95%
. По таблице «Значения критерия Стьюдента» при P = 95%  2,021. Так как,
2,021. Так как, 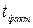 <
<  , нулевая гипотеза остается в силе. В ходе эксперимента не удалось статистически доказать разность между породами по массе. Осталось неизвестным, с чем связано различие между выборочными средними арифметическими (действительным различием между породами или случайными причинами).
, нулевая гипотеза остается в силе. В ходе эксперимента не удалось статистически доказать разность между породами по массе. Осталось неизвестным, с чем связано различие между выборочными средними арифметическими (действительным различием между породами или случайными причинами).
Эта задача может быть решена и другим способом – путем сопоставления доверительных интервалов генеральных средних (смотри пример 3.1). В рассматриваемом случае доверительные интервалы для первой и второй генеральной средней равны: 3,37  4,63 и 3,76
4,63 и 3,76  5,44 соответственно. Поскольку они перекрываются, нулевая гипотеза остается в силе.
5,44 соответственно. Поскольку они перекрываются, нулевая гипотеза остается в силе.
Пример 4.2. Предыдущее исследование было повторено на большем массиве особей. Полученные новые сводные показатели следующие:
| Группа | Объем выборки, n | Средняя арифметическая 
| Дисперсия 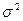
|
| Порода 1 | 4,1 ± 0,1 | 1,0 | |
| Порода 2 | 4,7 ± 0,1 | 1,0 |
Выдвигаем нулевую гипотезу 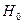 :
: 
Выбираем уровень доверительной вероятности P = 95%
Рассчитываем фактический критерий Фишера  .
.
Находим для каждой дисперсии число степеней свободы:  = 100 – 1= 99;
= 100 – 1= 99; 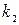 = 100 -1 =99. По таблице «Значение критерия F при различных доверительных уровнях» находим значение стандартного критерия Фишера
= 100 -1 =99. По таблице «Значение критерия F при различных доверительных уровнях» находим значение стандартного критерия Фишера  , которое равно 1,43. Так как
, которое равно 1,43. Так как 
 >
>  , нулевая гипотеза остается в силе.
, нулевая гипотеза остается в силе.
Переходим к сравнению средних арифметических.
Выдвигаем нулевую гипотезу 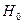 :
:  .
.
Рассчитываем фактическое значение критерия Стьюдента по выше приведенной формуле  .
.
Находим число степеней свободы для определения стандартного значения критерия Фишера, которое вычисляется по формуле k = 100 + 100 – 2 = 198. По таблице «Значения критерия Стьюдента» при P = 95% 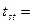 1,96, а при P = 99,9% (наивысшем уровне доверительной вероятности)
1,96, а при P = 99,9% (наивысшем уровне доверительной вероятности) 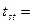 3,291.
3,291.
Так как, 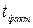 >
>  даже при наивысшем уровне доверительно вероятности, нулевая гипотеза опровергается.
даже при наивысшем уровне доверительно вероятности, нулевая гипотеза опровергается.
Решим задачу вторым способом – через доверительные интервалы, взяв за уровень доверительной вероятности P = 95%. При k = 99,  = 1,982. В рассматриваемом случае доверительные интервалы для первой и второй генеральной средней равны: 3,90
= 1,982. В рассматриваемом случае доверительные интервалы для первой и второй генеральной средней равны: 3,90  4,30 и 4,50
4,30 и 4,50  4,90 соответственно. В отличие от примера 14 они не перекрываются. Совершенно очевидно, что увеличение выборки привело к значительному увеличению точности эксперимента. Полученная разность оказалась достоверна с высшей надежность, значит, можно с уверенностью заключить, что индейки второй породы в среднем имеют большую массу, чем индейки первой породы.
4,90 соответственно. В отличие от примера 14 они не перекрываются. Совершенно очевидно, что увеличение выборки привело к значительному увеличению точности эксперимента. Полученная разность оказалась достоверна с высшей надежность, значит, можно с уверенностью заключить, что индейки второй породы в среднем имеют большую массу, чем индейки первой породы.
Пример 4.3. Требуется сравнить урожайность двух сортов нута за десять лет наблюдений. Результаты наблюдений и их первичная статистическая обработка приведены в таблице.
| Год | Урожайность в ц/га | Разница 
| 
|  
| |
| Сорт 1 | Сорт 2 | ||||
| 28,0 | 25,7 | 2,3 | -1,3 | 1,69 | |
| 21,3 | 12,2 | 9,1 | 5,5 | 30,3 | |
| 30,0 | 15,0 | 15,0 | 11,4 | 129,96 | |
| 15,0 | 18,0 | -3,0 | -6,6 | 43,56 | |
| 22,0 | 16,7 | 5,3 | 1,7 | 2,89 | |
| 18,1 | 17,1 | 1,0 | -2,6 | 6,76 | |
| 16,6 | 17,0 | -0,4 | -4,0 | ||
| 18,0 | 16,0 | 2,0 | -1,6 | 2,56 | |
| 22,1 | 19,2 | 2,9 | -0,7 | 0,49 | |
| 22,0 | 20,0 | 2,0 | -1,6 | 2,56 | |
| Сумма | 213,1 | 176,9 | 36,2 | – | 236,77 |
| Среднее | 21,3 | 17,7 | 3,6 | – | – |
В таблице приведены выборки с попарно связанными вариантами – несомненно каждый год имел свои специфические условия, которые одинаково влияли на урожай нута обоих сортов. В этом случае оценкой разности между генеральными средними будет средняя разность, определяемая из суммы разностей между попарно связанными вариантами сравниваемых выборок, т.е.

Оценкой генеральной дисперсии разности генеральных средних будет выборочная дисперсия
 ;
;  = 5,13
= 5,13
Ошибка средней разности равна:

Находим критерий  . Находим число степеней свободы для определения стандартного значения критерия, которое вычисляется по формуле k = n – 1 = 10 – 1 = 9. По таблице «Значения критерия Стьюдента» при P = 95%
. Находим число степеней свободы для определения стандартного значения критерия, которое вычисляется по формуле k = n – 1 = 10 – 1 = 9. По таблице «Значения критерия Стьюдента» при P = 95% 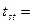 2,26. Так как,
2,26. Так как, 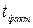 <
< 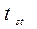 нулевая гипотеза остается в силе.
нулевая гипотеза остается в силе.
Таким образом нам не удалось доказать наличие статистически достоверной разности между урожайностью испытанных сортов нута по годам.
Пример 4.4. Изучалось влияние обработки сернистым газом на степень заражения фомозом корнеплодов моркови. При обработке сернистым газом заболело 82 из 1098 корнеплодов, без обработки – 639 из 1008. Таким образом, в опыте n  = 1098 p
= 1098 p  = 7%, в контроле
= 7%, в контроле  = 1008,
= 1008,  = 63%. Требуется оценить разность между долями в контроле и опыте.
= 63%. Требуется оценить разность между долями в контроле и опыте.
Оценкой разности между генеральными долями  служит разность между выборочными долями
служит разность между выборочными долями  . Ошибка разности между долями рассчитывается по формуле
. Ошибка разности между долями рассчитывается по формуле 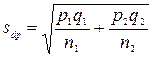 , где q = 1 – p или q = 100% – p. Отношение этой разности к своей ошибке дает величину критерия Стьюдента
, где q = 1 – p или q = 100% – p. Отношение этой разности к своей ошибке дает величину критерия Стьюдента  .
. 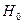 – гипотезу, или предположение о том, что
– гипотезу, или предположение о том, что 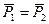 отвергается, если
отвергается, если  , для
, для  , при принятом уровне доверительной вероятности.
, при принятом уровне доверительной вероятности.
В рассматриваемом примере d = 63 – 7 = 56%. Ошибка разности между долями равна 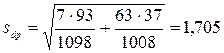 . Фактический критерий Стьюдента равен
. Фактический критерий Стьюдента равен  Стандартный критерий Стьюдента при k = 1098 + 1008 – 2 = 2104 и уровне доверительной вероятности 99,9% равен 3,291.
Стандартный критерий Стьюдента при k = 1098 + 1008 – 2 = 2104 и уровне доверительной вероятности 99,9% равен 3,291.
Так как,  при наивысшем уровне доверительной вероятности нулевая гипотеза отвергается. Обработка сернистым газом статистически достоверно снижает уровень заболеваемости фомозом корнеплодов моркови.
при наивысшем уровне доверительной вероятности нулевая гипотеза отвергается. Обработка сернистым газом статистически достоверно снижает уровень заболеваемости фомозом корнеплодов моркови.
Пример 4.5. Определение урожайности озимой пшеницы на 10 пробных площадях фермерского хозяйства дала следующие результаты: 35, 41, 39, 37, 45, 43, 36, 40, 42, 44 ц/га. Можно ли ожидать урожайность по всему хозяйству 43 ц/га, и какова вероятность этого события.
В данном случае требуется провести сравнение среднего арифметического выборки с гипотетическим значением генеральной средней. Предполагаем, что генеральная средняя равна конкретному числу а (в нашем случае 43), т.е. 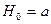 .
.
Фактический критерий Стьюдента рассчитывается по формуле:  , где
, где  – выборочная средняя арифметическая; а – конкретное число, которому равна гипотетическая генеральная средняя;
– выборочная средняя арифметическая; а – конкретное число, которому равна гипотетическая генеральная средняя; 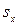 – статистическая ошибка средней арифметической.
– статистическая ошибка средней арифметической.
Рассчитываем значение средней арифметической  = 40,2 ц/га
= 40,2 ц/га
Находим значение дисперсии и среднего квадратического отклонения 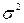 = 11,73;
= 11,73;  = 3,42.
= 3,42.
Ошибка средней арифметической равна 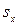 = 1,08 ц/га
= 1,08 ц/га
Находим фактический критерий Стьюдента 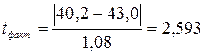 .
.
По таблице «Значения критерия Стьюдента» для доверительных вероятностей P = 95%; 99%; 99,9% при k = 10–1 = 9 находим соответствующие значения критерия  =
=  . Получаем, что
. Получаем, что 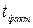 >
>  при Р = 95%, однако при Р = 99%
при Р = 95%, однако при Р = 99% 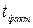 <
< 
 .
.
Таким образом, в целом по фермерскому хозяйству можно ожидать урожай озимой пшеницы равный 43 ц/га с доверительной вероятностью 95%.
Пример 4.6. Собранный с шести опытных делянок урожай зерна ржи варьировал следующим образом: 21,9; 24,6; 20,8; 25,1; 30,8; 23,2. Из приведенных данных выделяется варианта  = 30,8. необходимо проверить гипотезу
= 30,8. необходимо проверить гипотезу  о принадлежности сомнительной варианты к данной генеральной совокупности.
о принадлежности сомнительной варианты к данной генеральной совокупности.
Находим характеристики выборки:  = 24,4;
= 24,4;  = 62,14;
= 62,14; 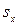 = 3,53.
= 3,53.
Рассчитываем фактический критерий Стьюдента 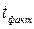 =
=  , где
, где  сомнительная варианта (дата).
сомнительная варианта (дата). 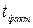 =
=  . В таблице для Р = 95% при k = 5 находим
. В таблице для Р = 95% при k = 5 находим  = 2,57.
= 2,57.
Так как, 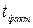 <
< 
 нулевая гипотеза остается в силе и сомнительная варианта не может быть выбракована из выборочной совокупности.
нулевая гипотеза остается в силе и сомнительная варианта не может быть выбракована из выборочной совокупности.
Вопросы для самоконтроля
1. Как формулируется нулевая гипотеза при сравнении двух средних арифметических?
2. Что такое критерий F?
3. В чем заключается нулевая гипотеза при сравнении дисперсий?
4. Можно ли считать достоверным различие между дисперсиями, если фактическое значение F больше табличного? Если оно меньше табличного?
Поиск по сайту: