ОСНОВЫ ДисперсионнОГО анализА

Цель – познакомить студентов с особенностями дисперсионного однофакторного анализа и алгоритмом решения задач по этой теме.

При решении задач, когда необходимо сравнить одновременно несколько выборок, объединяемых в единый статистический комплекс, целесообразно использовать дисперсионный анализ. Этот метод основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты, сравнивая которые, друг с другом посредством F -критерия можно определить, какую долю общей вариации учитываемого признака обуславливает действие на него как регулируемых, так и не регулируемых в опыте факторов.

Дисперсионный анализ позволяет:

1. Оценить силы и достоверность влияний факторов;

2. Оценить разности частных средних и частных долей;

3. Провести регрессионный анализ ряда частных средних и разработать прогноз развития признака при заданном комплексе условий;

4. Оценить гетерогенность родителей – степени разнообразия их наследственных способностей;

5. Оценить наследуемость признаков и определенных групп особей при передаче генетической информации из поколения в поколение;

6. Проанализировать комбинационные способности производителе, как основы планирования селекционной работы.

В дисперсионном анализе признаки, изменяющиеся под воздействием тех или иных причин, называются результативными. Причины, вызывающие изменение величины результативного признака, принято называть факторами. Факторы обозначают прописными начальными буквами латинского алфавита (А, B, C…), учитываемые признаки – конечными (X, Y, Z). На один и тот же признак действует много факторов, однако в опыте регулируются лишь некоторые из них: их называют регулируемыми или организованными факторами. Степени интенсивности фактора называются градациями фактора. Градации принято обозначать теми же буквами, что и факторы. Частные группы, подобранные для каждой градации фактора, называются градациями комплекса.

Если испытывают действие на признак одного регулируемого фактора, дисперсионный комплекс будет однофакторным, если одновременно исследуют действие на признак двух, трех или большего числа регулируемых факторов, комплекс называется двух-, трех- и многофакторным. Числовые значения (даты) результативного признака могут распределяться по градациям комплекса равномерно, пропорционально и неравномерно. Поэтому дисперсионные комплексы называют равномерными, пропорциональными и неравномерными.

Пример 6.1. При испытании новой минеральной подкормки на привес подсвинков организован однофакторный дисперсионный комплекс. Изучается несколько степеней действия фактора: пять увеличивающихся доз подкормки – нулевая (контроль), одинарная, двойная, тройная и учетверенная. Для каждой дозы в случайном порядке подобраны по нескольку подсвинков: для первой три, для второй четыре и далее пять, четыре, четыре. В результате получился дисперсионный комплекс, приведенный в таблице.

Градации фактора						q = 5
Даты,	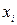2; 3; 1	4; 3; 6; 3	5; 6; 4; 6; 9	9; 7; 6; 6	3; 6; 5; 6
Объем градаций,						N = 20
Сумма дат						= 100
Частные средние

Это комплекс однофакторный, неравномерный. Объем комплекса N = 20, число градаций q = 5, повторности по градациям 3, 4, 5, 4, 4. – общая средняя по всему комплексу.

В однофакторном дисперсионном комплексе рассчитываются три дисперсии: факториальная, случайная и общая.

– факториальная (межгрупповая) девиата это сумма взвешенных квадратов центральных отклонений частных средних по градациям от общей средней по всему комплексу:

– случайная (внутригрупповая) девиата это сумма квадратов центральных отклонений каждой даты от своей частной средней: =

– общая девиата, сумма квадратов центральных отклонений дат от общей средней по всему комплексу: =

=

На основании трех девиат однофакторного комплекса можно засчитать показатель силы влияния фактора по следующей формуле:

или 60,5%

Ошибка показателя силы влияния находится по формуле:

Для расчета критерия оценки влияния (показателя достоверности влияния) регулируемого в опыте фактора на результативный признак необходимо найти соответствующие дисперсии:

– факториальная дисперсия равна факториальной девиате деленной на число степеней свободы (число градаций без одного q – 1).

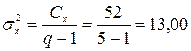
– случайная дисперсия равна случайной девиате, деленной на число степеней свободы (объем комплекса без числа градаций n—q)

– общая дисперсия равна общей дисперсии, деленной на число степеней свободы (объем комплекса без единицы N — 1)

Показатель достоверности влияния определяется по преобразованному критерию Фишера по формуле:

Стандартное значение критерия Фишера находим по таблице, пользуясь соответствующими степенями свободы:
и

При доверительных вероятностях 95%, 99% и 99,9% равен 3,1; 4,9 и 8,3 соответственно. Сравнив величины и при разных доверительных вероятностях установим, что фактический критерий Фишера больше стандартного при доверительной вероятности 99%, но меньше при доверительной вероятности 99,9%.

Таким образом, влияние минеральной подкормки на привес подсвинков за период наблюдения статистически достоверно при доверительной вероятности 99%.

После того, как достоверно установлено влияние регулируемого фактора на результативный признак, при необходимости прибегают к сравнению групповых средних друг с другом, как правило, контрольного (стандартного) и опытных вариантов.

Проведем сравнение контрольного варианта (градация 0) и опытного варианта (градация 3) групповые средние которых равны 2 и 7, соответственно. Для этого лучше использовать метод Шефе, который одинаково применим как к равно – так и неравновеликим по составу группам. Критерием достоверности различий, наблюдаемых между групповыми средними дисперсионного комплекса, служат следующие отношения:

(при );

(при );

Нулевая гипотеза отвергается, если

Для определения по таблице число степеней свободы и

Подставим в формулу имеющиеся значения

; и отсюда по таблице = 3,1 при P = 95%. Подставляем полученные значения в формулу и получаем 3,521. Так как , нулевая гипотеза остается в силе и разность между сравниваемыми вариантами опыта является статистически не доказанной. Очевидно, в дальнейшем необходимо увеличить объем выборочного комплекса.

Пример 6.2. Обычно, дисперсионный анализ дает возможность оценить силу и достоверность влияния факторов на какой-либо количественный признак, но может использовать и как показатель наследуемости. Чем выше показатель силы влиянии (), тем разнообразнее родители по своей способности давать лучшее или худшее потомство.

Посчитано количество щенков песца от разных самцов (А, В, С) у выровненного маточного поголовья самок. Данные приведены в таблице

Градации фактора	А	В	С	q = 3
Даты,	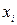1;2;3	4;6	7;8;9
Объем градаций,				N = 8
Сумма дат				= 40
Частные средние

Отсюда = 54; =6; = 60, соответственно ; ; .

Силу влияния фактора (в данном случае показатель наследуемости) определяем по формуле или 90%.

Показатель достоверности влияния определяем по критерию Фишера по формуле:

Стандартное значение критерия Фишера находим по таблице, пользуясь соответствующими степенями свободы:
и

При доверительных вероятностях 95%, 99% и 99,9% равен 5,8; 13,3 и 36,6 соответственно. Сравнив величины и при разных доверительных вероятностях установим, что фактический критерий Фишера больше стандартного при доверительной вероятности 99,9%.

Проведем сравнение плодовитости первого самца (градация А) и третьего (градация С) групповые средние которых равны 2 и 8, соответственно, по формуле: ;

Подставим в формулу имеющиеся значения

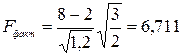; и отсюда по таблице = 5,8 при P = 95%. Подставляем полученные значения в формулу и получаем 3,405. Так как , нулевая гипотеза отвергается, т.е. статистически доказано, что у самца С потомство более многочисленное, чем у самца А.

Таким образом, анализ, проведенный по этой схеме, показывает, что исследованная группа самцов в высшей степени неодинакова по своим наследственным способностям (количеству щенков в потомстве). Для получения наибольшего количества щенков целесообразно использовать в качестве производителя самца С.

Вопросы для самоконтроля.

1. В чем заключается сущность дисперсионного анализа?

2. Из каких компонентов складывается фактическое отклонение варианты от средней арифметической при 1 контролируемом факторе?

3. Как установить достоверность влияния изучаемого фактора?

Поиск по сайту: