 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Взвешенная средняя арифметическая
Взвешенная средняя арифметическая используется тогда, когда значения вариант выборки имеют разный математический вес.
 , где
, где  – математический вес варианты (
– математический вес варианты ( ).
).
Пример 2.2. В кормовой смеси содержится следующее количество отдельных компонентов:
| Компонент | Содержание в смеси, кг | Содержание протеина, % |
| Сено | ||
| Резаная солома | ||
| Жмых подсолнечника | ||
| Пшеничные отруби |
Требуется определить содержание перевариваемого протеина в килограмме смеси.
Датами признака будет содержание белка в каждом компоненте, а их математическими весами – физические веса компонентов, находящихся в смеси.
Порядок работы:
1. Умножаются значения признака на их математические веса: 3·50+1·10+33·20+11·20 = 1040
2. Находится сумма математических весов компонентов (n) 50+10+20+20 = 100
3. Делим первое значение на второе 1040/100= 10,4% или 10%
Таким образом, в каждом килограмме кормовой смеси содержится 100 г перевариваемого белка.
Пример 2.3. Данные о продолжительности вегетационного периода сортов ячменя преобразованы в взвешенный вариационный ряд и представлены в таблице.
| Границы класса | Середина класса, 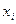
| Частота класса, 
| 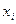 
|
| 57,5- 62,4 | |||
| 62,5-67,4 | |||
| 67,5-72,4 | |||
| 72,5-77,4 | |||
| 77,5-82,4 | |||
| 82,5-87,4 | |||
| 87,5-92,5 |
Требуется найти среднее значение вегетационного периода сортов ячменя.
В том случае, когда имеется взвешенный вариационный ряд, также может использоваться формула взвешенной средней арифметической, где:  – частота (математический вес) класса;
– частота (математический вес) класса; 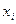 – середина классового интервала.
– середина классового интервала.
Расчеты производятся в следующем порядке.
1. Умножаем варианты на их частоты: 60·2 = 120 и т,д.
2. Суммируем эти произведения; 120+1950…680+360 = 16060.
3. Полученную сумму делим на объем выборки (n = 214)  = 16060/214= 75,1
= 16060/214= 75,1
Таким образом, продолжительность вегетационного периода составляет 75 дней.
Пример 2.4. Найдем общую среднюю арифметическую высоты растений гелениума осеннего за четыре года наблюдений по данным, приведенным в таблице.
| Год наблюдения | Средняя арифметическая, 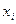
| Объем выборки,  
|  
|
Формула взвешенной средней арифметической используется и в случае необходимости получить общую среднюю составной выборки, для каждой, из отдельных частей которой средние арифметические уже известны.
Общая средняя будет равна:
 = 103 см
= 103 см
Пример 2.5. Рассчитайте медиану вегетационного периода статистической совокупности сортов ячменя по данным из примера 2.3.
Медианой называется варианта (или дата), разделяющая вариационный ряд на две равные по числу вариант части. Она рассчитывается по формуле:
 , где
, где  – медиана;
– медиана;  – начала класса, в котором находится медиана;
– начала класса, в котором находится медиана;  – величина классового интервала; n – объем выборки; L – сумма частот классов, предшествующих классу, в котором находится медиана;
– величина классового интервала; n – объем выборки; L – сумма частот классов, предшествующих классу, в котором находится медиана; 
 – частота медианного класса.
– частота медианного класса.
Рассчитаем медиану вегетационного периода совокупности сортов ячменя. Порядковый номер медианной варианты: 0,5 (214 + 1) = 107,5. Класс, в котором находится медиана, определяется путем накопления частот. Так, в таблице из примера 3 сумма частот сверху вниз равна: 2 + 30 + 34 + 62 = 128. Поскольку между 107 и 128 вариантами должна находиться медиана, накопление частот прекращаем и за начало медианного класса принимаем 72,5, т.е. меньшую границу класса: 72, 5 – 77,4, среднее значение которого 75, а частота 62.
Отсюда по формуле  = 72,5 +
= 72,5 +  дня.
дня.
Пример 2.6. Рассчитайте моду вегетационного периода сортов ячменя на основании данных таблицы из примера 3.
Модой называется точка на оси абсцисс, соответствующая максимальной частоте теоретической кривой распределения вариант. Вычисляется мода по формуле:
 , где Mo – мода;
, где Mo – мода;  – начало модального класса;
– начало модального класса;  – величина классового интервала;
– величина классового интервала;  – частота класса, предшествующего модальному;
– частота класса, предшествующего модальному;  – частота модального класса;
– частота модального класса;  – частота класса, следующего за модальным.
– частота класса, следующего за модальным.
Определим моду продолжительности вегетационного периода статистической совокупности сортов ячменя по выше приведенной формуле:
Mo = 77,5 + 
Поиск по сайту: