Вопрос 29. Средняя геометрическая и её определяющее свойство

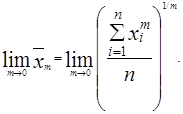В рассмотренных выше случаях, подставляя в общую формулу степенных средних различные значения порядка степенных средних m, мы получали формулы для их вычисления. Такой подход не годится для случая, когда m = 0. Попробуем найти предел, к которому стремится степенная средняя, если её порядок m стремится к нулю.

При 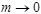выражение 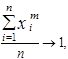а 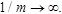Получаем неопределённость вида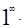

Для того, чтобы раскрыть эту неопределённость введём новую переменную

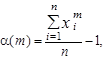которая стремится к нулю, при 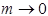. Так как 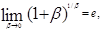то

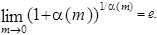Используя введённую переменную искомый предел можно переписать следующим образом:

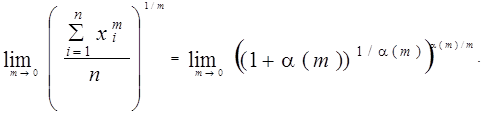Кроме того,

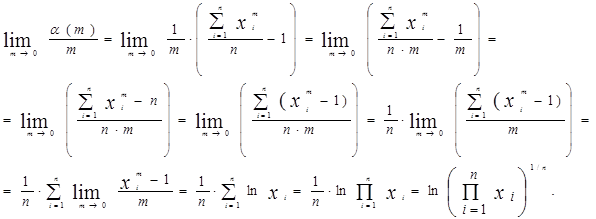
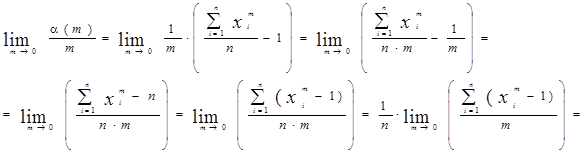
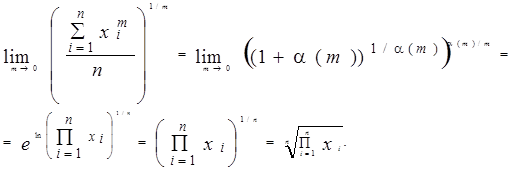Используя полученные выражения искомый предел можно переписать в виде:

Такой предельный случай степенной средней m -го порядка при 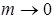и является средней геометрической величиной. Вычислить среднюю геометрическую в том случае, если исходные данные не подвергались первичной группировки, можно по формуле:

Если экспериментальные данные были предварительно сгруппированы, то среднюю геометрическую можно вычислить пользуясь формулой:

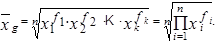В данном случае мы не можем сформулировать определяющее свойство по аналогии с рассмотренными выше степенными средними, так как сумма нулевых степеней наблюдений, как впрочем и любых других чисел, которыми они могли бы быть заменены, всегда равна числу наблюдений n. Однако анализ формулы для вычисления средней геометрической дает нам основание заключить, что если заменить все значения в выборке средним геометрическим, то произведение наблюдений не изменится, то есть справедливо равенство:

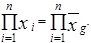Действительно, используя формулу для вычисления среднего геометрического правую часть данного равенства можно преобразовать следующим образом: 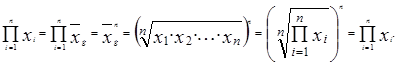Как правило, средняя геометрическая используется в тех случаях, когда анализируются темпы роста признака. Под темпом роста понимается отношение величины признака в какой-то момент времени к величине этого же признака в предыдущий момент учёта: 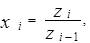где x_i - темп роста в i -й период времени, z_i - величина признака в i -й момент учёта (конец i -го периода времени), z_i-1 - величина признака в i -й момент учёта (начало i -го периода времени). При вычислении средней геометрической приходится находить произведение довольно большого числа сомножителей и вычислять корень такой же большой степени, что может привести к значительным трудностям. В связи с этим зачастую формулу для средней геометрической преобразуют путём логарифмирования левой и правой её частей и вычисляют логарифм средней геометрической.

Для не сгруппированного набора данных:

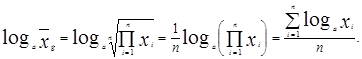
Для сгруппированного набора данных:

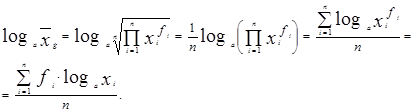Далее, путём потенцирования вычисленного логарифма находят среднюю геометрическую величину. Основание логарифма a может выбираться любым, но, как правило, используются десятичные или натуральные логарифмы. В том случае, если средняя геометрическая величина вычисляется для темпов роста какого-либо признака, вычисленных для последовательных равных периодов времени, то можно воспользоваться более простой формулой.

или 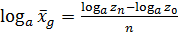, где z₀ - значение признака в начальный момент учёта, z_n - значение признака в конечный момент учёта. Действительно, подставляя выражение для темпов роста в среднего геометрического получим:

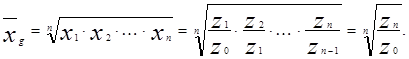
Поиск по сайту: