Вопрос 25. Свойства средней арифметической величины

1. Сумма отклонений вариант от средней арифметической величины равна нулю. Действительно

Используя формулу средней арифметической получим:

2. Если к каждому наблюдению прибавить константу c, то и среднее арифметическое изменится соответствующим образом. Покажем это.

.

3. Если каждое наблюдение умножить на константу c, то среднее арифметическое изменится аналогичным образом. Действительно

.

4. Сумма квадратов отклонений вариант от их средней арифметической величины меньше, чем сумма квадратов отклонений от любой другой величины, то есть

для любого . Чтобы доказать это, покажем, что выражение достигает минимума в точке

Продифференцировав сумму квадратов отклонений по a получим:

Далее найдём, в какой точке производная принимает нулевое значение:

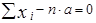откуда И

Отсюда следует, что сумма квадратов отклонений имеет один локальный экстремум в точке . Так как вторая производная этой функции по a в точке равна положительному числу:

, то в точке функция имеет минимум.

5. Средняя арифметическая величина ряда, состоящего из двух групп наблюдений равна средневзвешенной из средних значений групп наблюдений с весами, равными объёмам групп:

Покажем это. Используя формулу среднего арифметического, правую часть равенства можно преобразовать следующим образом:

В общем случае, когда ряд наблюдений состоит из k групп, средняя арифметическая величина всего ряда равна средневзвешенной арифметической групповых средних с весами, равными объёмам групп:

6. Средняя арифметическая величина для суммы или разности взаимно соответствующих значений признаков двух рядов наблюдений с одинаковым числом наблюдений равна сумме или разности средних арифметических значений этих рядов.

Распространяя данное свойство на сумму или разность k групп с одинаковым числом наблюдений можно сказать, что их общая средняя арифметическая равна сумме или разности средних арифметических групп:

Поиск по сайту: